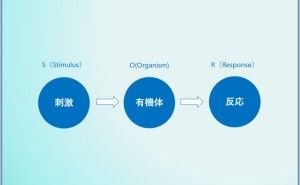
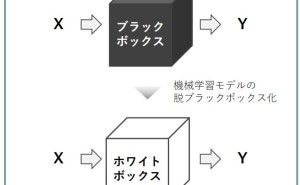
新QC7つ道具とは、QC活動の高まりとともに次第に製造以外にも拡大した結果、'60年代末頃から主に生産現場改善で数値統計に使われていたQC七つ道具に対し、定性/言語情報の分析に対するニーズが高まり、日科技連主導の元'72年から新しいツールの検討が始まり、'77年に管理者・スタッフのために発表されたもので、N7(New7toolの略)とも呼ばれます。 その中身は、親和図法、連関図法、系統図法、マトリックス図法、アローダイアグラム、PDPC法、マトリックスデータ解析法の七つであり、 品質管理(QC)というよりは、品質改善、業務改善の計画用途で使用されます。今回は定性的な分析手法の多い新QC7つ道具の中で、定量分析にどっぷりつかっている「マトリクス解析法」について説明します。
- 親和図法
- 連関図法
- マトリクス法
- 系統図法
- アローダイアグラム
- PDPC法
- マトリクス解析法 ← 今回の説明対象
1. QC7つ道具と新QC7つ道具
QC7つ道具とは、数あるものづくり技法の中でもまず思い浮かびます。 '50年代から活発化したQC活動の流れの中で、誰でもやさしく理解できるツールを体系化するために、弁慶の7つ道具になぞらえて'60年代末頃からQC7つ道具と呼ばれるようになりました。 パレート図、特性要因図、グラフ、チェックシート、ヒストグラム、散布図、管理図の7つです。グラフの代わりに層別が入ることもあります。それに対して新QC7つ道具は、QC7つ道具と同様に品質管理で利用されている分析手法です。QC7つ道具は主に製造現場向けですが、新QC7つ道具は営業部門や企画部門などに対象範囲を広げたものです。どちらかというと、定性データの分析に向いています。
営業部門や企画部門などでは、数値化しにくい定性的な情報(例:テキストや頭の中にあるアイデア、エライ人の考え、現場の雰囲気など)を扱うことが多いためです。問題を解決するにあたって、ものづくりの現場はもちろん、企画や管理、営業部門において、数値データに対して情報の多くは言葉で表現される“言語データ”が扱われます。言語データから有益な情報を抽出し、新しい発想を生み出してくれるツールが「新QC七つ道具(N7)」ですQC7つ道具と同様、統計の専門家でもデータ分析の専門家でもない現場の人が使っています。
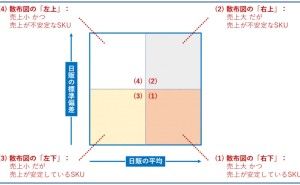
2. マトリクス解析法とは
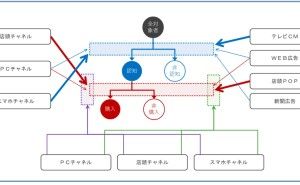
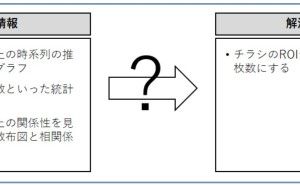
マトリクス解析法は、他のQC7つ道具や新QC7つ道具と異なり、分析ツールを使ったほうがいいでしょう。扱うデータは、次のようなExcelなどのスプレッドシートを彷彿させるようなデータです。
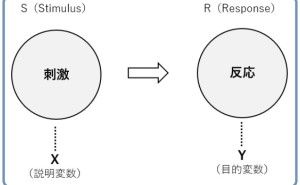
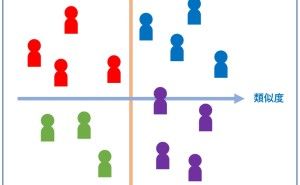
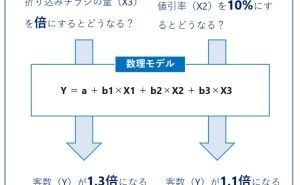
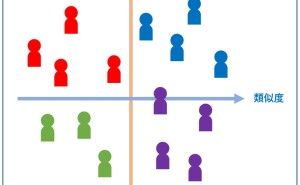
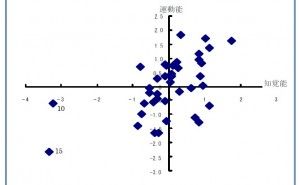
多数の数値を計算・整理するにあたり、説明変数同士の相関をもとに、できるだけ少数の指標で記述し、それを平面上に表す手法で、多変量解析の主成分分析と呼ばれるものです。 手順としては説明変数間の相関行列を作り、説明変数と同数の主成分を定義し、それぞれの寄与率を評価する事で、各主成分の意味を考えます。 特徴的な2つの主成分軸で各サンプルを評価すると、当初の説明変数で比較するよりもそれぞれの特徴を一層際立たせることが可能になります。
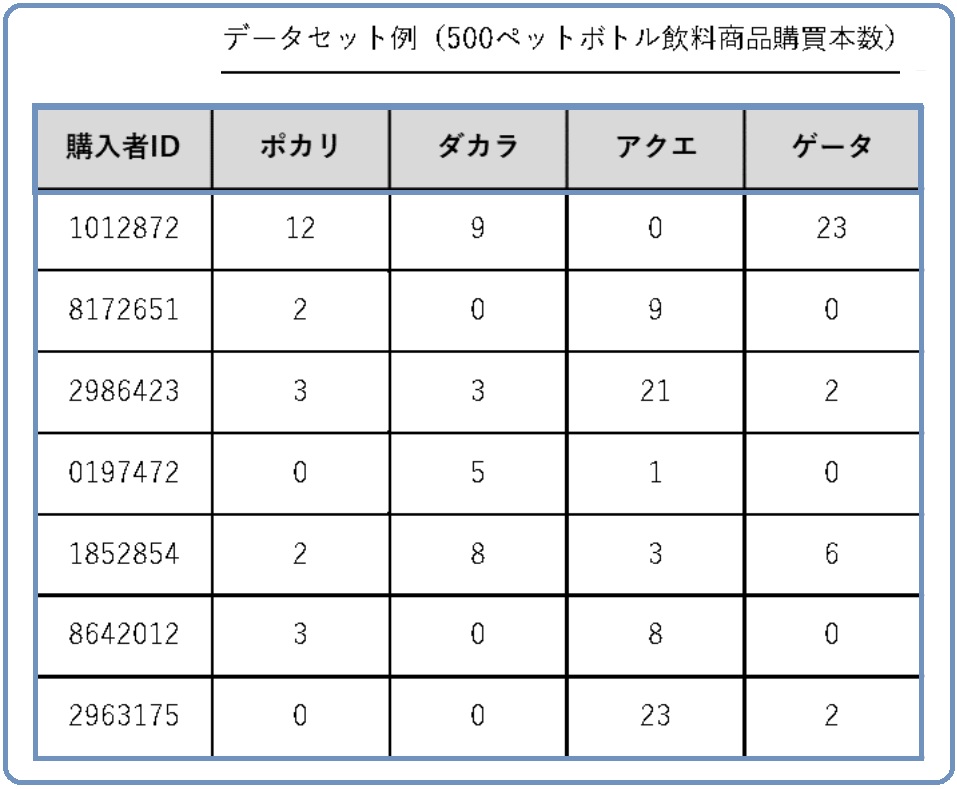
通常はデータセットと呼ばれます。伝統的には、多変量解析などの統計モデルを使い分析を進めます。
3. 多変量解析
伝統的な多変量解析の分析手法だけでも、例えば次にように沢山あります。
- 単回帰分析/重回帰分析
- 判別分析
- ロジスティック回帰分析(2項/多項/順序)
- プロビット回帰分析
- 正準相関分析
- 主成分分析
- 回帰分析
- クラスター分析
- 多次元尺度構成法
- コレスポンデンス分析
- 多段層別分析
- 数量化1類/2類/3類/4類
- パス解析
- グラフィカルモデリング
- 共分散構造分析
従来からある分析手法のため書籍も多く、活用事例も多くあります。
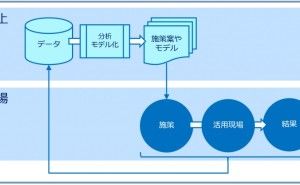
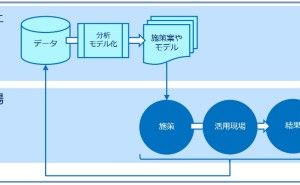
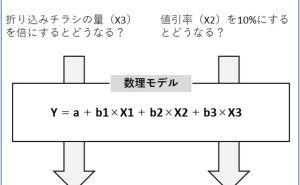
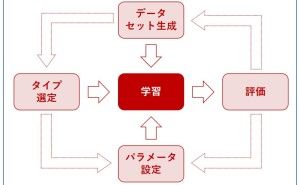
4. 伝統的な多変量解析の数理モデルを構築しよう
実務でデータ分析・活用を考える時、伝統的な多変量解析を使った方が良いでしょう。理由は、比較的分かりやすく、教科書や参考になる情報も多く、適応事例や実務上の実績もあるからです。
もちろん最近流行りだした……
・ニューラルネットワーク系のディープラーニング
・決定木(ディシジョンツリー)系のXGBoost
……など比較的新しい手法を使うのも良いでしょう。
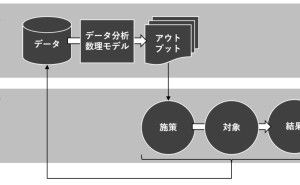
5. 数理モデルの厄介なところ
数理モデル(予測モデルや異常検知モデルなど)の厄介なところは、新しい手法の方が素晴らしい結果を出すかというと、そうでもないところです。
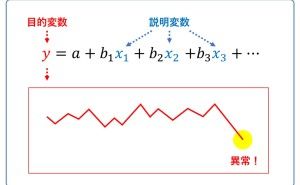
実務で売り上げなどの数値を予測する数理モデルの場合、ディープラーニングやXGBoostなどで苦労して構築した予測モデルが、昔からある多変量解析の重回帰分析で構築した予測モデルに精度で劣る、という現象を何度か目の当たりにしています。
仮に予測精度で勝っても、それほどでもない場合も多々あります。
それほどでもないとは、例えば予測精度が1%アップしたところで、そこから導き出された結論やアクションなどに差異がないということです。予測精度1%アップにかけた時間と費用と情熱が報われないということです。
6. 伝統的な多変量解析で十分なケースが多い
実務上は、伝統的な多変量解析で十分なケースが多いようです。
例えば、次のように分析を進めると良いでしょう。
・まずは、分かりやすい多...