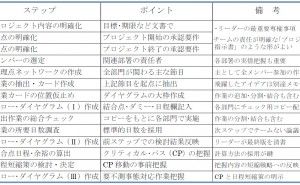
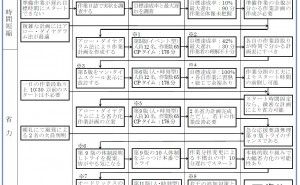
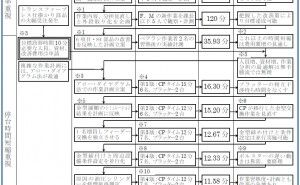
第8章 アロー・ダイヤグラム法の使い方
8.4 挑戦計画立案のためのアロー・ダイヤグラム法の基本ステップ
8.4.2 挑戦計画立案のためのアロー・ダイヤグラム法の基本ステップ
前回のその6に続いて解説します。
Step 12:結合点日程・余裕の算出
アロー・ダイヤグラム法の対象である挑戦計画は、最大の不確定要素である挑戦内容とその関連事項が最もうまくいったときのものとしているので、ネットワークが完成した時点で、経験的にCPが把握されることが多いのです。そのような場合は、無理に算出する必要はなく、CP上の作業の詰めと管理に注力するべきです。ただ、日程がタイトと思われるパスがいくつもあったり、当初から、日程短縮が第一義の目的だったりすると、この算出が必須となります。
その場合、作業日程計算表を用いた説明が一般的ですが、作業数が多くなると、作表そのものが煩雑で、多大な工数を計算のみに取られてしまうので、この連載では、ネットワーク上で直接算出・記入する方法を紹介します。この方法の場合、算出プロセスがそのまま、日程短縮策模索に必須の“ネットワークの詳細把握とチェック”につながるので、リーダーがじっくり取り組むことをお勧めします。日程計算の必要性があるような、日程的にタイトなプロジェクトの場合は、たとえソフトがある場合でも、そちらは検算と心得て、この方法を実行するだけの価値があります。以下に詳細を説明します。
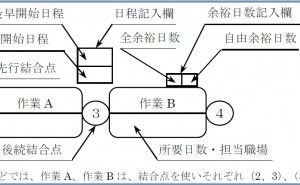
【ポイント 1】最早開始日程(ES:Earliest Start time)の計算と記入
最早開始日程というのは、先行作業との関係も含めて、その作業を開始できる最も早い日程のことで、第1結合点ではゼロです。最早開始日程を計算する作業の先行作業すべてについて次の計算を行い、最も大きい値がその作業の最早開始日程であり、計算は第1結合点からスタートします。
ES=(先行作業の最早開始日程)+(先行作業の所要日数)
まず、最も注意しなくてはならないのは、先行作業を漏れなく抽出することで、比較的複雑な作業Nの場合は、近いものから順に、K、J、Mの3つです。次に、抽出した3つの作業(K、J、M)の最早開始日程は、各作業の先行結合点(Kは⑦、Jは⑥、Mは⑧)の日程記入欄の上段にある、26、22、24です。各作業の所要日数は、作業カードの下段に書かれており、Kは7、Jは6、Mは2です。以上2種類の数字を加えたものが各作業のESの値です。
ESK=26+7=33 ESJ=22+6=28 ESM=24+2=26
上記3つのうちの最大値“33”が、“作業Nの最早開始日程”であり、結合点⑨の上の日程記入欄の上段に記入する。ちなみに、ここで求めたESの値が小さいほど、その先行作業は余裕があるということになります。
【ポイント 2】最遅開始日程(LS:Latest Start time)の計算と記入
最遅開始日程というのは、後続作業が、最遅開始日程に作業を開始できるためには、その作業の開始を遅くともその日に始めなくてはならない日程のことであり、計算は最終結合点からスタートします。最遅開始日程を計算する作業の後続作業すべてについて次の計算を行い、最も小さい値がその作業の最遅開始日程です。
LS=(後続作業の最遅開始日程)-(当該作業の所要日数)
当該作業と先行結合点が同じ作業を漏れなく抽出すること、作業Lの場合は、もう1つ作業Kが存在します。次に、それら両作業(L、K)の後続作業(P、N)の最遅開始日程は、各作業の先行結合点(Pは⑩、Nは⑨)の日程記入欄の下段にある34と33です。各作業の所要日数は、作業カードの下段に書かれており、Lは3、Kは7です。各作業のLSの値は、後続作業の最遅開始日程から、各作業の所要日数を引いた値です。
LSL=34-3=31 LSK=33-7=26
上記2つの内の最小値“26”が、“作業Lの最遅開始日程”で、結合点⑦の上の日程記入欄の下段に記入します。ちなみに、ここで求めたLSの値が大きいほど、その作業は余裕があるということになります。
【ポイント 3】全余裕日数(TF:Total Float)の計算と記入
全余裕日数とは、ある作業が日程的に取り得る最大の余裕日数のことで、その作業が属するパス(経路)の持つ全余裕日数と言い換えることができます。すなわち、その作業が属するパスにおいて、先行作業のすべてが最早開始日程にスタートして所要日数で作業を完了し、後続作業のすべてが最遅開始日程にスタートして所要日数で作業を完了するという特殊な状態のときに、その作業が取り得る余裕です。したがって、全余裕日数を利用する場合は、関係する全作業との事前調整が必要です。作業Xの全余裕日数(TFX)は、次式で求めることができます。
TFX=(Xの後続作業の最遅開始日程)-(Xの最早開始日程+所要日数)
作業Fの最早開始日程は作業Fの先行結合点③の日程記入欄の上段の“16”で、所要日数は、作業カードの下段にある“6”です。次に、後続作業(J、I)の最遅開始日程は、後続結合点⑥の日程記入欄の下段にある“27”です。以上の数字を当てはめると、“作業Fの全余裕日数(TFF)”は、
TFF=27-(16+6)=5
から“5”となり、作業カード右上の余裕日数記入欄の左側に“5”を記入します。ちなみに、この値が“0”のとき、その作業はCP上にあります。
【ポイント 4】自由余裕日数(FF:Free Float)の計算と記入
自由余裕日数とは、ある作業が、後続作業とは無関係に使用できる余裕日数のことで、文字通り、その作業が自由に使うことができる余裕日数です。すなわち、その作業が属するパスにおいて、後続作業のすべてが、最早開始日程で作業を開始することを前提にした上で、認められる余裕日数であり、作業Xの自由余裕日数(FFX)は次式で求められます。
FFX=(Xの後続作業の最早開始日程)-(Xの最早開始日程+所要日数)
作業Fの最早開始日程は作業Fの先行結合点③の日程記入欄の上段の“16”で、所要日数は、作業カードの下段にある“...