第8章 アロー・ダイヤグラム法の使い方
8.4 挑戦計画立案のためのアロー・ダイヤグラム法の基本ステップ
8.4.2 挑戦計画立案のためのアロー・ダイヤグラム法の基本ステップ
前回のその5に続いて解説します。
Step 10:作業の所要日数調査
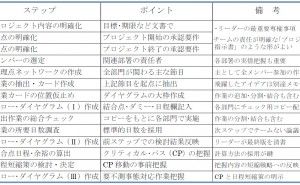
これは、前ステップでの抽出作業の総合チェック結果を念頭に、自部署関連の作業についてアロー・ダイヤグラム(Ⅰ)の作業名の下の欄に記入する。
自分たちの首をしめることになる数字だということで、できるだけ余裕を持たせるようなセクショナリズム的発想は排除しましょう。やってみなければ分からない要素の多い挑戦的な作業については、すべてうまくいった場合の数字を記入し、不確定要素については、第9章で取り上げる「不測事態への対応計画作成」の必要作業として登録しておきます。
【ポイント 1】関係者合意の“これならいける”という数字でよい
この時点では、よほどのことがない限り厳密な調査をする必要はありません。厳密な所要日数調査は、Step13における日程計算の結果、日程短縮の必要性が発生した時点で、プロジェクトの進捗に直結するクリティカルパス(CP:Critical Path)上の作業について実施すればよいのです。
【ポイント 2】折り合いつかない場合は“3点見積法”の推定平均値をとる
「不測事態への対応計画作成必要作業」ほどではないが不確定要素があり、関係者が合意する所要日数が得られない場合です。“3点見積法”というのは、PERTにおいてプロジェクトの納期達成度を確率計算で求めるため、各作業の所要日数の平均値と分散を見積もる方法で、次のようにします。
まず、所要日数を検討し、次の3種類を求める。
- 最短値(Optimistic Time) a:予想される最短日数
- 最尤値(Most likely Time) m:最も可能性の高い日数
- 最長値(Pessimistic Time) b:予想される最長日数
上記3つの値が、a:m:b =1:4:1の割合で発生するものとして、推定平均値(μ)は次式で求めます。
μ=(a+4m+b)/6
分散(σ2)は、分布が正規分布に近似し、aとbの隔たりが6σと仮定して、次式で求めます。
σ=(a‐b)/6
上記2つの式の前提をみても分かる通り、積極的な根拠があるとはいえないのですが、計算しやすい上、これらの式を用いて結果的に大した誤りがないことが経験的に分かっていますので(注8-2)、公式化されています。結果的に大した問題がないのは、経験的に85%の作業は余裕日数を持っており(注8-3)、残りの作業の遅れを吸収できるのと、クリティカルパス(CP)が明確になるので、CP上の作業は、休日や時間外による作業ごとの調節がなされることが背景にあります。
逆にいえば、所要日程の見積りに厳密さを求めるよりも、ネットワークの作成を優先し、把握したCP(2次、3次も含む)上の作業の日程短縮や管理の充実に注力すべきということです。
(注8-2)(注8-3)「PERT入門」刀根薫著(東洋経済新報社)前者P.130、後者P.110
Step 11:アロー・ダイヤグラム(Ⅱ)の作成
アロー・ダイヤグラム(Ⅰ)の原紙(作業カードを仮止めした状態)を使って、Step9、10での入手情報や検討結果を反映したネットワークをカードの仮止めで作り、コピーします。
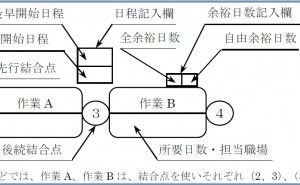
コピーしたネットワーク図に、先行結合点の結線、ダミー、指定期日などの記入をした後、結合点日程記入欄、余裕日数記入欄を記入します。
【ポイント】カードは仮止め状態とし、コ...