【目次】
第5章 マトリックス・データ(MD)解析法の使い方←今回
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第5章 マトリックス・データ(MD)解析法の使い方
5.1 MD解析法について
5.1.1 多変量解析法の主成分分析法
本章では、第1章で定義した、スタッフワークレベルの“混沌C”、すなわち、“環境変化に伴い、求められる総合評価基準が変化したために起こる混沌”を解明するための、マトリックス・データ解析法(以後MD解析法)の使い方を説明します。
現在の産業界は、ITを核とする技術革新と、米国主導のグローバルスタンダード化の流れを受け、明治維新に匹敵するといわれる諸規範の激変を余儀なくされ、その対応に混迷を極めています。
戦後幾多の難関を突破してきた産業界が難渋を強いられているのは、過去経験した難局は、日本独自のプロセスで極めた製品の品質、性能、コストにおける競争力で切りぬけることができましたが、今回は、そのプロセスそのもののあり方を問われているところにあるでしょう。
すなわち、背景である政治体制、産業構造も含めて、企業そのもののあり方を問われており、まさしく、“環境変化に伴い、求められる総合評価基準が変化したために起こる混沌”といえ、まさにMD解析法の出番であり、その的確な活用による現状打破が望まれるところです。
しかしながら、このMD解析法は、N7の中で唯一数値データを扱うものである上、そのオリジナルがSQCの中でも難解とされる多変量解析法の主成分分析法そのものであることから敬遠され、あまり活用されていないのが実情です。
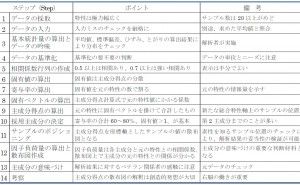
したがって、連載での説明では、MD解析法をより身近なものとして的確な活用ができるためのガイドとなることを主眼としました。具体的には、計算は身近に充実している計算ソフトを使うという前提で、数理については他書に譲り、説明の主眼を次の3点に置くことにしました。
(1) SQC手法におけるMD解析法の位置づけ
「重回帰分析まではともかく、そこから先はちょっと…」という認識だった筆者が「そうか、そういうことだとMD解析法を避けるということは“ある種のスタッフワークの放棄”を意味するのか。なら、本腰入れてみよう」に変わったきっかけの説明。
(2) マトリックス・データに対する無手勝流アプローチ事例
多くの側面を持つ解析対象を把握しようとすると各側面に対するサンプルごとのデータ、すなわちマトリックス・データ(MD)と対峙することになるが、無手勝流アプローチのなれの果てを筆者の経験をベースにした“セミドキュメンタリーストーリー”に託し、“MD解析法の核心を身近なものとして把握”できた経緯を説明します。
(3) 同上事例をもとにMD解析法の各解析ステップの意味づけ
無手勝流ではあるがMDと真剣に対峙した上記取り組みで、試行錯誤の繰り返しの果てに行き着いた「解析対象を的確に把握するにはMDを“どのように処理すべきか”は分かったが“どう処理したらよいか分からない”」に対する解決策としてのMD解析法を、無手勝流取り組みと対比しながら説明します。
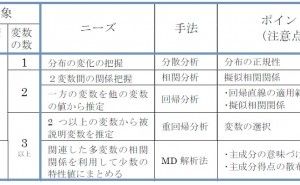
5.1.2 MD解析法(多変量解析法の主成分分析法)とは
前述したように、多変量解析法の中の主成分分析法(Principal Component Analysis: PCA)そのものです。詳しくは事例をもとに後述しますが、次のように定義づけすることができます。
「多種多様の特性からなる複雑な事象がある場合、これらの事象に対応して測定された多変数の相互関連を分析活用し、少数の総合的特性値にまとめることによって、複雑な事象の見通しと把握を容易にする手法である」
この定義をかみ砕いて説明すると次のようになります。
要するに、複雑な事象には、いろいろな側面があるので、その事象を把握しようとしても、手に入るのは、それぞれの側面を代表する多くの特性値がサンプルごとに求められる“マトリックス・データ”であり、普通の取り組み方では、気になるいくつかの特性値を個々に評価するのがせいぜいです。ところが、個々に評価してみて気づくのは、それらの特性値が互いに独立していることはまずなく、特性値相互の相関関係の存在です。
そこで、その相関関係に着目して数学的処理をほどこし、互いに独立した新たな特性値を、元の特性値との関係も含めて求める手法が“MD(マトリックス・データ)解析法”の数理に関する核心です。
この新たな特性値は、計算上は元の特性と同じ数だけ求められますが、情報量の多いものから順番に取り上げると、2番目か3番目までで、全体の6~8割の情報をカバーするのが通常です。
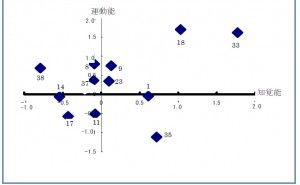
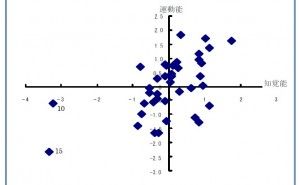
したがって、これら2~3の新たな特性値を、対象事象を把握するための“総合特性値”として採用し、2次元の座標軸上に各サンプルの値をプロットしてみると、複雑でとらえどころのなかった事象を総合的に把握できるとともに、各サンプルについても、プロットされた位置関係により、その特徴がかなり明確に把握できるので、複雑な事象への対応に見通しを立てることができるわけで、ここまでの処理を含めた総合的な解析手法が“MD解析法”です。
定義の説明に長文をあてたのは、まず最初にこのような把握をしておくことは、結構複雑な今後の具体的な説明の、“断片的、局視的な把握”ではなく、“手法の大筋を構成する部分としての把握”を可能にし...