第4章 親和図法の使い方 ←今回
第5章 マトリックス・データ(MD)解析法の使い方
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第9章 PDPC法の使い方
第10章 PDCA-TC法の使い方
新QC七つ道具:第4章 親和図法の使い方
4.2 混沌解明のための親和図法の基本的ステップ
【参考文献について】文中( )内の意味
参考文献に頼る機会の多い本節では、次のような工夫をして、参照を容易にしたのでご活用願います。すなわち、参照すべき個所の表示を、参考文献は、参考文献リストのローマ字、参照ページはその後に続く数字で表わし、( )でくくることにしました。ということで、まず、活用する参考文献を、ローマ字の符号をつけて下記に紹介します。G、H、I以外の著者は、川喜田二郎氏です。
A 「発想法」中公新書No.136
B 「続・発想法」中公新書No.210
C 「問題解決学」講談社
D 「知の探検学」講談社現代新書No.476
E 「パーティー学」社会思想社現代教養文庫
F 「KJ法 」中央公論社
G 「カンの構造」中山正和著 中公新書No.174
H 「管理者・スタッフの新QC七つ道具」日科技連出版
I 「新QC七つ道具の企業への展開」日科技連出版
J 「チームワーク」光文社(カッパブックス)
K 「経営のためのKJ法 入門」日本能率協会編
4.2.1 混沌解明のプロセス、14のステップ
本節から、スタッフワークレベルの“混沌B”、すなわち、“現システムのレベルが低いために起こる混沌”を解明するための親和図法の使い方の説明に入ります。説明の仕方としては、連関図法の場合と同様、筆者が体感した“余法をもって代え難い感じ”を伝えるために、2通りの方法を準備しました。
まず最初は、混沌解明のプロセスを14のステップに整理し、その各々をうまくこなすためのポイントを、KJ法の諸文献との関連も考慮して解説し、普遍的な説明をします。次に、事例を通じて、スタッフワークに親和図法を活用する上での勘どころ、さらには、筆者独自の活用法について言及します。
特筆すべきは、筆者が23年前、第1回新QC七つ道具研究会(略称:1N7研)で完成させたA型図解と、それと同じデータに今回再挑戦したA型図解との違いの中から、親和図法に関する兼ねてよりの疑問点に言及した点です。その疑問点というのは、連関図法のところでも言及しましたが、言語データを扱う手法の場合最も気になる“結論に対する解析者の影響度”ですが、その点に関し、今回の経験を通じて得た結論について説明するので参考にして下さい。
4.2.2 混沌解明のステップとポイント
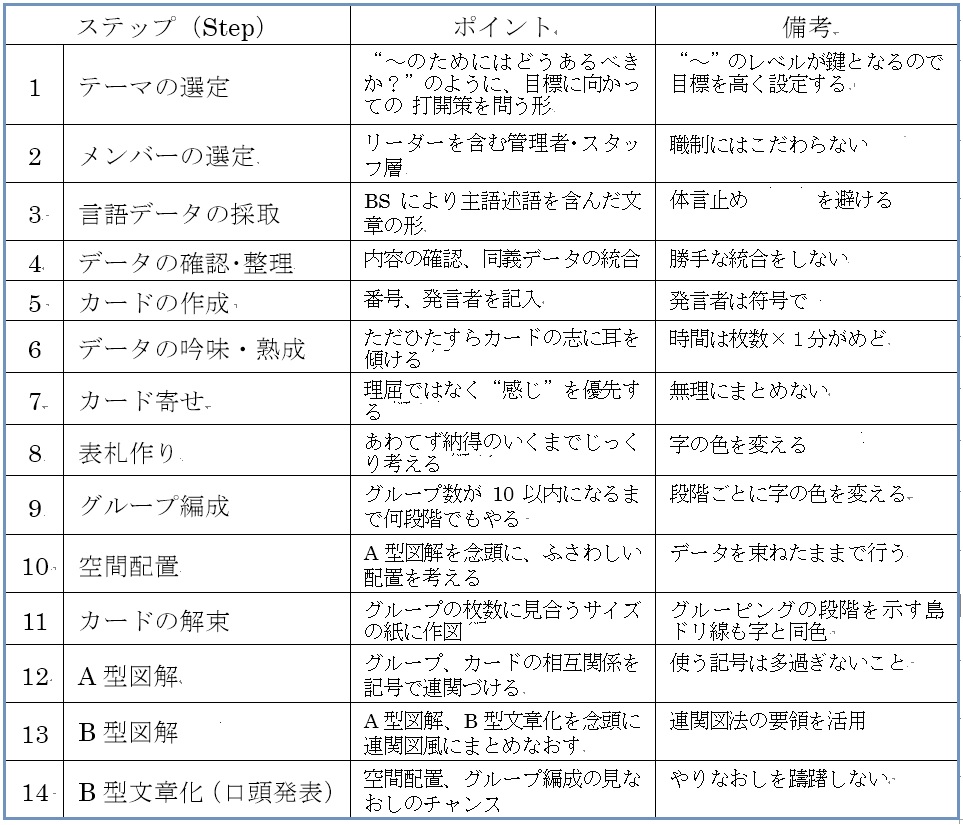
まず、全貌を把握してもらうために、14のステップと各々のポイントを、若干の説明を付して一覧表にまとめたのが、表4-2です。
表4-2 親和図法による混沌解明のステップとポイント
この内容は、筆者の諸体験をもとに、普遍化を意識して取りまとめたものです。ただ、今回時間をかけてレビューした結果、新たに気づいたり、発見した内容も、若干の検証と確認を経て追加しました。
ステップが既版のN7書やKJ法の解説書と異なっているのは、経験した勘どころを説明しやすくするためであり、内容的には既版のものをカバーしています。また、ステップの名称に耳慣れない言葉が使われていますが、これは、筆者が実感したことを伝えやすい言葉を選んだためです。
表に対する注記の中には、後述する各ステップの詳細内容説明と重複するものもありますが、この時点で大枠を理解してもらうことを優先し、重複を恐れず記載しました。
親和図法の場合は、連関図法と違い、オリジナルである“KJ法 ”の完...