「検定・推定」の記事検索
13件中 1~13件目
-
検定推定を行う手順とは
【目次】 今回は、次の事例をもとに、検定推定を行う手順を解説します。 1. 二つの母分散の比に関す... -
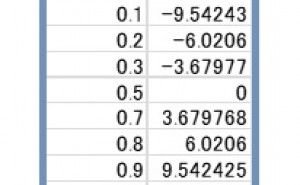
Ω(オメガ)変換とは
1. Ω(オメガ)変換が必要な理由 歩留り90%のものを95%にするのは、歩留り30%を60%にするより難しいといいます。これは元々よいも... -
コスト改善と、有意差検定
コスト改善と聞いてどの様な取り組みをイメージしますか、一般的にはコストダウンと絞り込んだ方がわかりやすいかもしれません。製造業で言えばある製品を一個造る... -
改善してる?~『 誤差の悲劇 』
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤... -
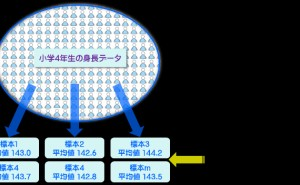
プロセスのばらつきと測定のばらつき
データ分析を行う上でばらつきの評価は避けて通れません。同じ手順で実施しているつもりでも実際は微妙に異なりばらつきが発生します。そのばらつきを出来るだけ小... -
母比率の区間推定 - 視聴率の一喜一憂 -
統計的区間推定は%などの比率データにも適用できます。比率データとして代表的なものに視聴率データがあります。予備知識としてビデオリサーチ社のウェブサイト情... -
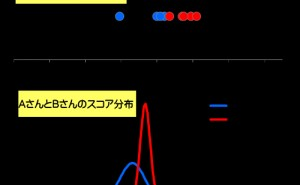
有意水準、5%の考察
統計的有意差検定とは一定確率の元で◯×判定を下す手法です。この一定の確率を『有意水準』と呼びます。有意水準とは危険率とも呼ばれ逆に100%から危険率を... -
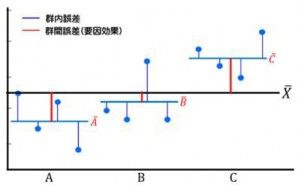
群内誤差と群間誤差 (その2)
前回のその1に続いて解説します。群内誤差が大きければ群間誤差(要因効果)が観えなくなるので、単純に平均値だけでの評価は危険が伴います。それは郡内誤差が群... -
群内誤差と群間誤差 (その1)
統計学を学ぶ最大の利点の一つは、『効果と誤差』についての理解ができることです。逆に言えば改善アクションを行った時、効果と誤差を区別出来なければ、それが意... -
統計的区間推定
1.統計的推定とは 統計的処理の基本に検定と推定があり、検定とは一定の確率の元で行う◯×判定、言わば定性評価で、推定とは◯×の... -
統計的有意差検定と有意水準をわかりやすく解説
【目次】 1.表が出やすいコインの判定と有意水準 有意差の判定を、コイントスの事例で考えてみましょう。普通のコインな... -
統計的有意差検定とは
1.検定と推定 統計学はデータを数量化して母集団の特徴や傾向を分析したり、母集団からサンプルを抜き取り、この中から母集団の特徴を推測する科学的な学...