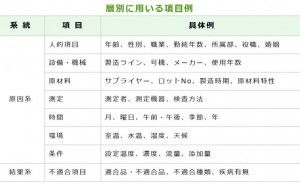
1．ヒストグラムとは
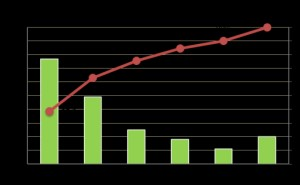
ヒストグラムとは、数量化データを大きさに応じて幾つかの区間にグループ分けし、各グループに所属するデータ数(度数)を棒グラフで表したものです。 区間に対して度数がどの様に分布するかを表したグラフなので、分布の形から母集団の特徴を分析できます。
解りやすい様に実例で説明しょう。英語の試験を40人が受験した結果が、以下の様になりました。
英語試験の点数(100点満点、受験者数40人)
35 37 41 47 53 56 62 66 72 39
44 49 55 59 64 67 43 46 51 57
61 42 48 53 58 63 48 54 60 61
49 55 57 50 52 56 50 54 51 52
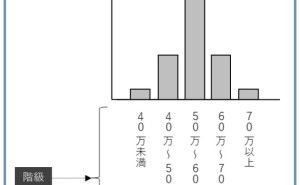
これを5点刻みの区間で該当者を振り分けると下の様になりました。 横軸に点数区間、縦軸に該当者数(度数)の棒グラフを書くと図1の様になります。
区間 人数
30点未満 0
31-35点 1
36-40点 2
41-45点 4
46-50点 8
51-55点 10
56-60点 7
61-65点 5
66-70点 2
71-75点 1
76点以上 0
図1．試験結果のヒストグラム
この例で点数の範囲をヒストグラムでは"区間幅"、人数を"度数"と言います。
2．ヒストグラムの作成方法
上記のヒストグラムは理解しやすい様に5点刻みの区間で描きましたが、データ数とデータレンジに基づいて区間数や区間幅を決めます。その値から区間開始と区間中央の値が決まりヒストグラムを作成します。
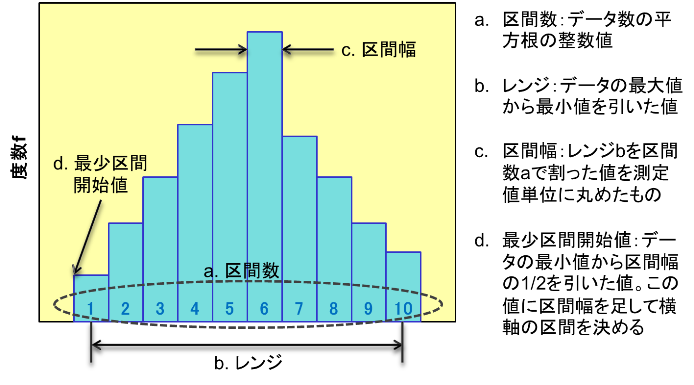
ヒストグラムの分布の形状から、複数の母集団の存在(層別の必要性)や異常の有無、特定要因によるばらつきや規格に対する工程能力を知る事が出来ます。また規格値を一緒に記すことにより、規格に対してどの様に分布しているか、また片寄りが無いかを確認出来ます。
3．ヒストグラムの形状パターン
分布の形状として代表的なものをいくつか紹介します。
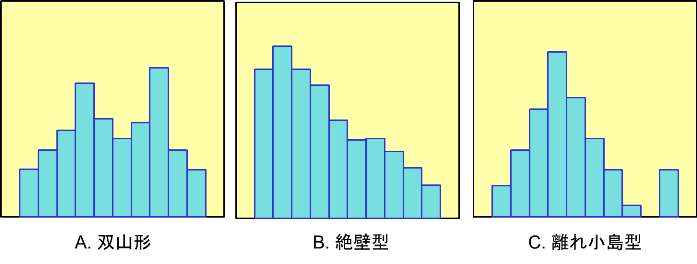
図3．ヒストグラムの分布パターン1
- 双山型 分布に二つの山があり、異なる分布が混在している
作業者による違い、製造装置の違い等で生じる - 絶壁型 分布が左右均等にならず、片方に分布の山が極端に寄っている
欠陥個数など片側がゼロ以上と制約を受ける場合等で生じる - 離れ小島型 分布から離れて飛び値が見られる
突発的な工程異常、測定ミス等のデータが含まれている.
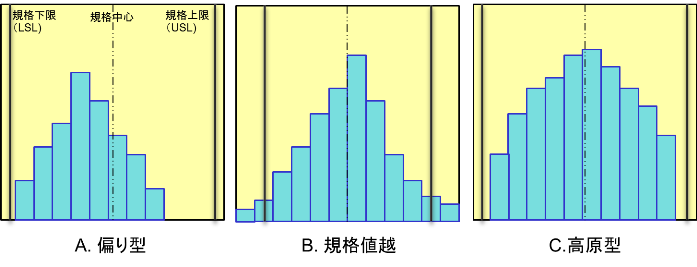図3．ヒストグラムの分布パターン2
- 偏り型 規格値センターに対し分布の中央が左右どちらかに偏っている
狙い値のセンタリングが上手く出来てない場合に生じる - 規格値越え 分布の裾が規格値を超えてしまっている
ばらつ...
