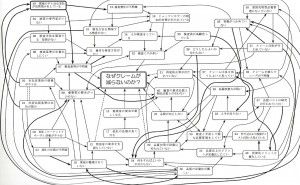
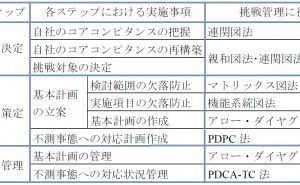
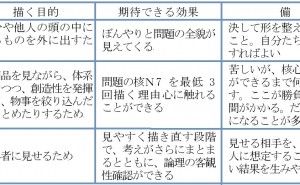
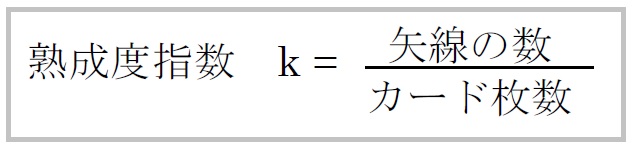第3章 連関図法の使い方
3.1 連関図法について
前回の3.1.3 連関図法のオリジナル手法についてに続いて解説します。
3.1.4 使用対象について
(1) 連関図法の使用対象には2種類ある
連関図法は、上記開発経緯からも分かる通り非常に柔軟性を持った手法で、使用対象も幅広い範疇をカバーし得る手法である。しかし、解析の難しさという点から使用対象を見てみると、“やるべきことはある程度分かっているが、優先順序、もしくは、だれが(または、どの部署が)やるべきかがはっきりしない場合”と“やるべきことそのものが、ランダムに多すぎて手のつけようがないケースも含めて、はっきりつかめない場合”の2種類に大別することができる。今後の説明のため、前者を“使用対象A”、後者を“使用対象B”とする。
(2) 本書で取り上げるのは“使用対象B”
“使用対象A”の場合は、連関図法開発の契機となった事例がその典型といえるが、関係者の生の声が等しく同じ俎上に上った段階で、目的のかなりの部分が達成されているといっても過言ではない。すなわち、主眼は連関図作成過程における関係者間の、やるべきことの優先順序と担当についてのコンセンサス作りにある。一方、“使用対象B”の場合は、問題解決ための“問題点の絞り込み”が主眼となるが、筆者の経験では“使用対象A”に対するのと同程度の取り組みでは不十分で、連関図そのものをさらに深く追求する必要がある。しかし、“連関図を深く追求する”とはどういうことかとなると難しく、筆者なりに工夫して活用してきた“指標”を、その後の検証結果も含めて次項で紹介する。
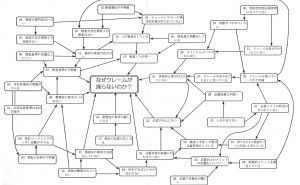
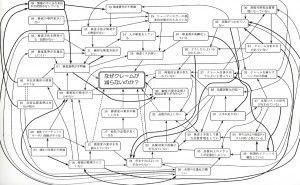
3.1.5 連関図はどこまで追求すればよいのか?
(1) 「親和図法」にあり「連関図法」にないガイドライン
先に述べたように、スタッフワークレベルの問題に連関図法を適用するには“連関図を深く追求すること”がポイントである。しかし、“深く追求する”といっても、どこまで追究すればよいのか、すなわち“連関図がどのような状態になればよいのか?”という素朴な疑問に答える何らかのガイドラインが必要である。
その点、次章で取り上げる「KJ法」をオリジナルとする「親和図法」の場合は、「カード寄せをした束が一匹狼のカードも1つと数えて、数束、多くても10束になるまで」というガイドラインが存在する。
親和図法に取り組むと夜を徹することが多いのは、このガイドラインがなかなかクリアできないからであるが、そのおかげでしかるべき結論を手にすることができるというのが筆者の実感するところである。したがって、「連関図を深く追求することとは?」という問いに答えるには“連関図法にもこれに相当するガイドラインを考案する必要がある”というのが、連関図を知った当初からの筆者のテーマであった。そういった考えのもと、長年の検討を経て到達した結論を以下に紹介する。
(2) “熟成度指数k”の採用
連関図を深く追求しつづけ、結果としてしかるべき結論を手に入れた後振り返ってみると、その追求の過程は“熟成”という言葉が一番ふさわしいと感じている。
したがって、「連関図を深く追求する」とは「連関図の熟成の度合いを高める」と言い換えることができ、その度合いを示す指標を手に入れることができればよいことになる。
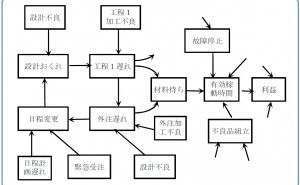
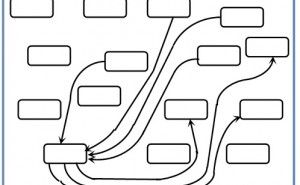
そこで、連関図の追求度合いを示す尺度を何にするかを考えたとき、最初に浮かぶのが“矢線の数”であろう。しかし、“矢線の数”は、当然のことながら、カード(言語データ)の数が多ければ追求の深さとは関係なく多くなってしまうので、矢線の数をカードの枚数で除した値を“熟成度指数k”と命名し、ガイドライン設定の指標として使うことにした。
(3) 経験則からのガイドライン:k = 1.8
熟成度指数という命名は最近であるが、この考えそのものはかなり早い時点から頭にあり、連関図法使用に際しては、常に意識して取り組んできた。
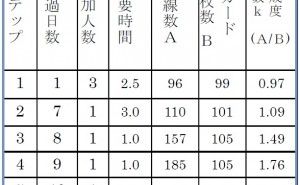
その結果、スタッフワークに連関図法を使用した場合、問題点の核心が見えてくるタイミングが、不思議にkが1.8 前後であることに気づいた(Engineers No.440 P.25表3で提案)。
その後、数多くのスタッフワークに対する連関図使用を通じて検証を重ねてきたが、そのタイミングはいずれもk=1.8前後に収まっており、親和図法における「カード寄せした束が10以下」に相当する連関図法のガイドラインとしての有効性に確信を持つに至ったのである。
しかし、ここで問題なのは、この経験則があくまで筆者独自の経験によるものであり、客観的な説得材料に欠ける点である。ただ、過去の経験から世の中に何らかの客観的検証材料が存在するのではないか、との確信に近いものを実感していたが、先に紹介した複雑系の書物の中にそれを発見したのである。
この発見がうれしく、ガイドラインに関する一連の経験則とともに日科技連の機関誌Engineerに投稿したところ採用になったのが、本書執筆のきっかけです。このような経緯を経て、本書ではスタッフワークを使用対象とした場合の連関図追求のガイドラインを「熟成度指数k=1.8」としている。
次回は、3.1.5 (4) 連関図の熟成度曲線...