第3章 連関図法の使い方
3.1 連関図法について
前回の3.1.5 連関図はどこまで追求すればよいのか(3)に続いて解説します。
(4) 連関図の熟成度曲線が示す“熟成過程の基本パターン”
スタッフワークに連関図を使用して感じるいま一つの経験則は、乗り越えるのに大変な困難を感じる節目の存在と、時間的経過に則した“共通した熟成パターン”の存在です。そこで、ある使用事例においてその点を意識し、熟成度指数の時間的経過を把握してみたところ、表3-1のような結果を得ました。これをグラフにしたのが 図3-2です。これは一事例のグラフですが、筆者の経験からいえることは、このグラフの時間軸のスケールは事例により変化するのですが、起伏の基本的な形状は共通、ということです。また、過去に接した事例のほとんどが、k = 1.0を少し超えたところ、すなわち、最初の平坦部である「1次熟成」で終わっているのは、“使用対象A”の場合は、k=1.0が、ガイドラインということです。
表3-1 熟成度指数の推移
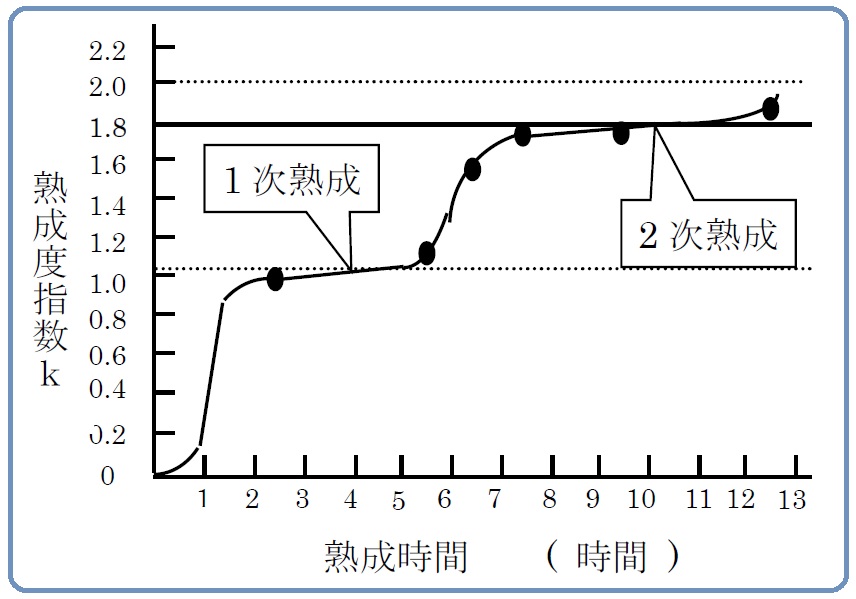
図3-2 熟成度曲線
(5) 連関図法と親和図法とではガイドラインの持つ意味が違う
前項で、連関図法のガイドラインk=1.8を、親和図法におけるガイドライン「カード寄せした束が10以下」に相当するものと説明しました。しかし、それはあくまで、“解析者を挫折することなく、問題解決の糸口をつかむところまでガイドするための手段”としての“相当”であって、手法における位置づけとしては、親和図法のそれとは、似て非なるものです。そこで、両手法におけるガイドラインの持つ意味の、共通点と相違点を以下に取りまとめ、k=1.8の持つ意味を再確認しておきます。
ⅰ)両手法に共通していえる点
双方とも、“採取した言語データ”という限られた情報源をもとにした深い思考により、問題の全体像を把握した上で、その核心を解明し適切な解決策の糸口を導き出す手法です。ところが、実際に取り組んでみると、全体像把握までのめどが立たない不安感から、思考不十分なままで結論を急ぎ、手法の持ち味を生かしきれないことが多いのです。そういった事態を避けるために、結論把握のタイミングと相関を持つ分かりやすい指標を用いて、「結論を得るためには、少なくともここまで頑張ってみることが必要である」と指し示している点が両手法のガイドラインに共通する点です。これを違った角度からみると、これらのガイドラインは、各手法のアウトプットである“親和図”や“連関図”の「問題の全貌把握ができた時点での特徴」から読み取った経験則といえます。したがって、両ガイドラインに共通していえることは、ガイドラインをクリアすれば、与えられた情報を最大限に活用した“問題の全貌把握”が可能になるという経験則を示している点です。
ⅱ)親和図法のガイドラインの持つ意味
親和図法の場合は、個々のデ-タが、カード寄せプロセスを経て発展的統合を繰り返すことにより、不足情報を発展的に補いつつ核心を絞り込むことができる上、そのプロセスと結論の核心が、アウトプットである親和図上に表札カードとして表現されます。したがって、親和図法の場合は「ガイドラインのクリアは、手法の使命達成に直結する」という位置づけです。また、解析者の思考プロセスは、親和図上に表札カードとして思考の順序を追った形である程度残るので、もたらされた結論は解析者以外にも比較的理解しやすいのが特徴です。
ⅲ)連関図法のガイドラインの持つ意味
連関図法の場合は、個々のデータ間の論理的関連を矢線の結合で徹底的に追求することにより、解析者の脳裏において、不足情報の補填と問題の核心の絞り込みがなされるが、そのプロセスは、明確な形としては連関図上には現れてこないのです。したがって、連関図法の場合ガイドラインの位置づけは“解析者を挫折することなく問題解決の糸口をつかむところまでガイドするための手段”ということになり、親和図法と大きく違うのです。それゆえ、連関図法の場合はガイドラインをクリアしただけでは手法の使命達成とはいかず、「不足情報の補填」と「問題点の絞り込み」を、解析結果(連関図)との関連において別途明確にする必要がある。この点は、連関図をスタッフワークに適用する場合の重要なポイントです。筆者独自の経験則の域を出ないものの、試行錯誤の上それなりの検証を経て到達した結論を次項での使い方の中で説明します。
3.1.6 おわりに
この連載では、第1章で使用対象の観点から連関図法に興味を抱かれた方に、何とか使ってみようという気になっていただくことを念頭に注力しました。すでに使ったことのある方は、筆者の経験に思い当たる節がおありでしょうから、比較的...
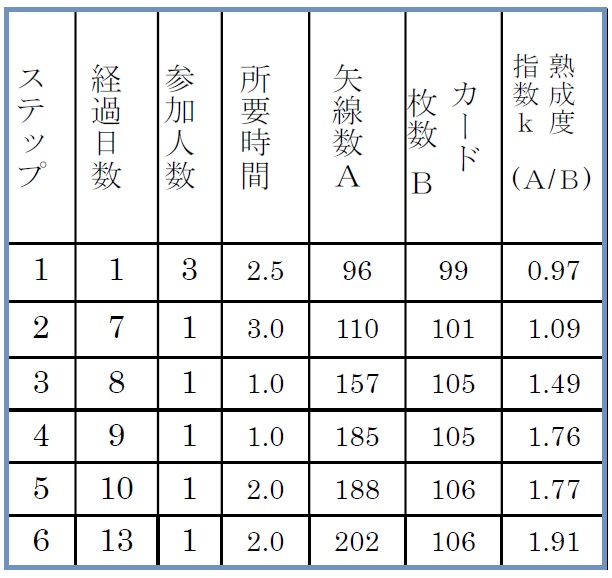
 図3-2 熟成度曲線
図3-2 熟成度曲線

 図3-2 熟成度曲線
図3-2 熟成度曲線
 図3-2 熟成度曲線
図3-2 熟成度曲線