【目次】
第3章 連関図法の使い方 ←今回
第4章 親和図法の使い方
第5章 マトリックス・データ(MD)解析法の使い方
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第9章 PDPC法の使い方
第10章 PDCA-TC法の使い方
新QC七つ道具:第3章 連関図法の使い方
前回に続いて、3.2.3 各ステップの詳細説明のStep 14から解説を続けます。
Step 14:最終連関図の作成
連関図は、一応、ステップ10で完成していますが、リポートに添付する最終版は、衆目にさらされるので体裁を整えるのと、往々にしてリポート作成時のレビューで発生する若干の加筆修正を反映する必要があります。また、連関図だけでも、ある程度結論が分かるようなガイダンスを盛り込み、リポートによる本格的な理解への誘導をねらうのです。
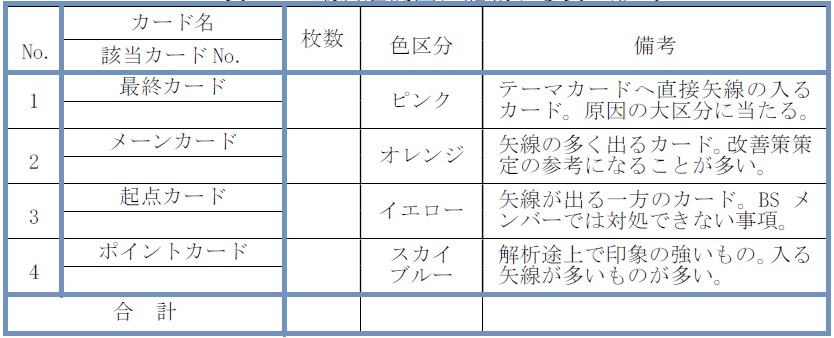
【ポイント 1】4種類のカードの説明を一覧表の形で記入して連関図の見方をガイドする。
現在のところ、表3-4のような表を連関図の右上のスペースに記載するのを標準にしています。色区分は、筆者が標準にしているものを書いたまでで特にこだわる必要はないでしょう。備考欄には、一般的なことを記入してありますが、該当する連関図の理解を助ける内容の記述をこれに加えるとよいでしょう。
表3-4 最終連関図に記載する表の形式
3.2.4 連関図法による結論の客観性
スタッフワークレベルのテーマの場合、データ採取を的確に行うと、データ数は少なくとも100前後(筆者の経験では286が最大である)になります。毎回、途方に暮れる思いを何度も経験しながら、何とか最終結論に至ることができたのは、混沌の本質を把握したいという強い執念に加えて、N7研の1期生としての責務ともいえる意識が根底にあったことが大きいのです。それに支えられる形で、最後には必ず“余法をもって代え難いもの”を強く感じるところまで頑張れたように思います。
本節は、筆者を支えた“N7研1期生”といった特殊要因とは縁のない読者の方々に、この実感を味わってもらいたいとの強い思いを込めて準備しました。いざ取り組んでみると、悪戦苦闘の日々がまざまざと蘇り、それにつれ、伝えたいことが怒涛のごとく現われ、ずいぶん紙面を割いてしいました。読み返してみて、くど過ぎてかえって分かりにくくなったのではないかとの危惧も禁じ得ないのですが、上述の思いをお汲み取り願い、読者のご賢察によりカバー願えることを期待しています。また、内容的に、文章だけでは伝えきれないもどかしさを随所で感じましたが、それらの点は、次節の具体例による説明において補足します。
・連関図法による結論の客観性
連関図法をスタッフワークに活用する上で気になることの一つは、最終連関図から抽出した結論の客観性、すなわち普遍性と妥当性です。この点は連関図法活用当初から念頭にあり、諸検討を重ねて到達した筆者なりの結論が、Step13の「6種類の主要カードとの関連を軸とした“結論のリポート作成”」といえます。
したがって、次節でご紹介する事例では、特にその点を強く意識して挑戦したが「結論の核心を引き出す最終段階では、普遍性との対極である強い主観的判断を避け得ない」との実感は、過去の諸事例と軌を一にするものです。
そこで、あらためて過去の諸事例を、そういった観点からレビューしてみて感じるのは、N7の活用対象であるスタッフワークそのものが、本来解析者の主観に頼る面が強いものであり、SQCにみられるような普遍性を求めるべきものではないのではないかということです。とはいうものの、ここでの主観は個人的なものであってはならず、テーマが関わる主体(会社や部門)の方針に沿うものでなければならい点はいうまでもなく重要なポイントです。
いま一つの、妥当性であるが、最終解析者の個人的力量に左右される面が大きく不安感はより強いといえよう。とするならばそれらの検証が問題になるのですが、その結論を受けて具体的な改善活動を実施する関係者は、通常テーマに関する背景や目的を熟知しているので、結論に従った実施段階において的確な検証がなされ得ると考えてよいのではないだろうか。したがって、トップを含めた関係者は結論を鵜呑みにすることなく、その点を念頭に置いて事に当たるべきでしょう。
連関図法により手に入れた結論が関係者の検証に堪え得ないケースとしては、解析不足と採取データの不適格が考えられ、本章では特にその点に注力したつもりです。ただ、現状に詳しくないトップや新任の上司、特殊な例としてコンサルタント、といった人にとっては解析結果の検証は無理な相談です。
この点について、特に解析不足に対する客観的な検証という点で強い関心と期待を寄せているのが、猪原正守氏(大阪電気通信大学) の“DEMATEL(Decision Making Trial & Evaluation Laboratory)法を適用した連関図法への数値解析の導入に関する研究”(注3-19)であることを付記しておきます。
(注3-19)「新QC七つ道具事例集(Ⅳ)」日科技連(1990年9月) ...