パラメータ設計の後で，製造で問題が起こらないように，図面寸法やスペックの公差を決める許容差設計と許容差の決め方を解説します。これはまた，材料や部品の取引をするための規格値の決め方についても活用できます。

1．許容差設計

1.1　許容差設計の目的　

　パラメータ設計は低コストの部品を使って，SN比で機能性や品質特性を改善する手法ですが，品質改善の目的はコスト改善ですから，品質とコストをバランスさせて，品質改善の効果をコストに還元することが最も大切です。

　もしパラメータ設計でSN比を 6db改善できれば，ばらつき（標準偏差や劣化係数）が 4倍の低コスト部品や材料を使っても，製品のばらつきは変わらないことになるのです。この場合，半分の 3dbを品質改善に，残り半分の3dbを部品や材料コストの改善に回すことによって，製品の価格を半分にすることができます。許容差設計は，「品質改善の成果をコスト改善に還元させる手法」でもあるのです。

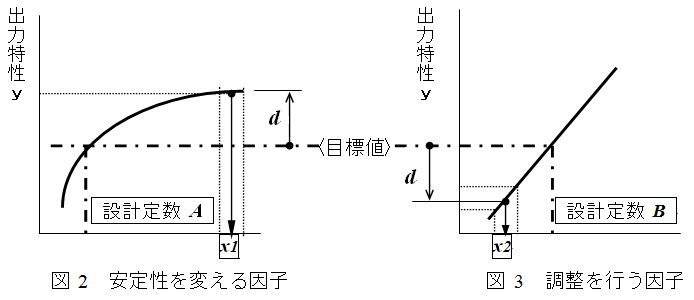
　図1は，特性値とコストの因果関係を表したものですが，品質は目標値から離れると増大し，コストは逆に減少することが分かっています。特性値がA,B,Cの3種類で，コストと品質の比較をすると，特性Aは，部品コストが品質コストより大きくなりますから，企業の利益を圧迫することになります。特性Bは，品質コストが部品コストより大きくなりますからから，市場でクレームが多発することが予測されます。特性Cは，部品コストと品質コストがほぼ同じで，全体の社会的損失コストは最小になります。

　このことは，原発事故でも分ったことですが，投資コストと市場における損失コストがバランスするシステムを設計することが大切なのです。

特性A： コスト≫品質 で利益を圧迫

特性B： コスト≪品質 で損害が多発

特性C： コスト≧品質 で品質とコストがバランスして全損失が最小になる

全損失（L円）＝品質(Q)＋コスト(C) 

1.2 許容差設計の説明

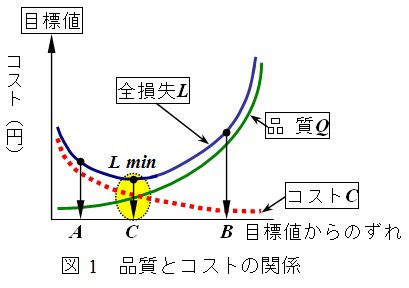
　パラメータ設計では，図2と図3に示すように設計定数Aの非線形性を利用し，飽和領域を選ぶことにより出力特性の安定化を図り，その後で目標値mとの差dを設計定数Bで調整して，制御因子（設計定数）の最適条件を求めます。

　しかし，設計定数の値（x1とx2）がばらついたら出力特性もばらついてしまうのです。

そこで許容差設計では，設計定数と出力特性の因果関係を明らかにして，｢設計定数のばらつきの限度（許容差）｣を決めて，図面寸法やスペックの許容差を決めて設計を完了して，製造部署に引き継ぐことになります｡

1.3　許容差設計の手順事例

　あるOA機器メーカーで，読取り装置の駆動に使われるプーリのコストダウンの要求が製造から出され，材質変更の検討をすることになりました｡

　商品の画像品質は，プーリの外径寸法が±0.28mmずれたら画像に伸びがでて駄目になり，そのとき市場におけるお客の修理費用は 4万円位かかることが分かっています｡   そこで，次のようなステップで許容差設計を行い，品質損失と部品コストがバランスするように最適な材料を選択します｡

ステップ1　グレードの選択　

部品の精度（等級）や材料の種類など許容差のグレードを決めるものをリストアップします。

　　　　　　　 表1　材料の種類のリスト

ステップ2  損失関数Lの選定

　部品の特性や組立品の品質特性から「損失関数」を決定します。

    望目特性　L=k(y-m)² 　⇒　　沢山の試料の場合は　L=kσ²

  　望小特性　L=ky²　　　　　　　　　　　　　　　　　　　

　　望大特性　L=k/y²

　ステップ1の材料や抵抗の選択の場合，望目特性の損失関数を用います。

表1の材料の規格（許容差）⊿=0.15の場合，標準偏差σ=⊿/3=0.05とします。

ステップ3　機能限界Δ0と損失A0の決定

　「機能限界Δ0」は，顧客の半分の人が機能を果たさなくなると感じる限界で，この限界を LD50（生と死が50対50）と呼びます。

　この問題では，⊿₀=0.28mmです。また，「損失A0」は，この機能限界を越えたときの市場での損失の平均値（機能が復帰するのに必要な修理費などで代用する）を求めます。この問題では，A₀＝40,000円です。

ステップ4　比例定数kの計算

　望目特性と望小特性はk=A₀/⊿₀²　，望大特性は k=A₀⊿₀² 　で求めます。

　この問題では，k=40,000/0.28²=510.204（円/mm²）になります。

ステップ5　部品コストA0と損失コストLの計算

　部品の各許容差ごとに，部品コストAと損失関数を使った損失コストLを計算します。表2のように計算結果をまとめます。

   　　　　　　　　　　　　表2 品質とコストのバランスの計算

ステップ6　総合コスト L の計算

部品コストAと損失コストLを加えた総合コストL_Tを計算します。

ステップ7　総合コストが最少のグレードの選定

　総合コストが最少のグレードを選定します。

　この問題では，アルミニュウムAが総合コストが最少ですから，アルミニュウムAを選定します。最初は，アルミニュウムBを選んでいましたから，年間10万台造る予定として，たった一部品だけで（1005.7-741.7）×100,000＝2640万円の合理化ができることになります。

以下，【後編】につづく