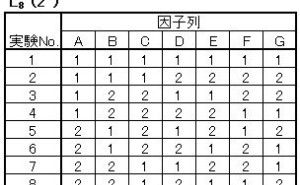
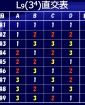
直交表で各因子水準のデータを平均するだけで要因効 表1.L8直交表の配列
果が算出できることを、L8(27)を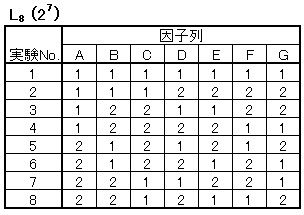 使ってやや数理的に解説してみましょう。
使ってやや数理的に解説してみましょう。
L8の各因子の水準配列は右の表1になります。7因子2水準のデータ構造モデルとして、全体の平均値μに対して因子Aの第1水準と第2水準データx1 、x2を下のように考えます。
x1=μ+a1 (因子A第1水準の効果)+e1(誤差=実験誤差+測定誤差)
x2=μ+a2 (因子A第2水準の効果)+e2(誤差=実験誤差+測定誤差)
ここで a1+a2=0 になることに注意して下さい。
するとL8直交表の8列のデータx1~x8は下のような構造になります。
x1=μ+a1+b1+c1+d1+E1+f1+g1+e1 …………(1)
x2=μ+a1+b1+b1+d2+E2+f2+g2+e2 …………(2)
x3=μ+a1+b2+c2+d1+E1+f2+g2+e3 …………(3)
x4=μ+a1+b2+c2+d2+E2+f1+g1+e4 …………(4)
x5=μ+a2+b1+c2+d1+E2+f1+g2+e5 …………(5)
x6=μ+a2+b1+c2+d2+E1+f2+g1+e6 …………(6)
x7=μ+a2+b2+b1+d1+E2+f2+g1+e7 …………(7)
x8=μ+a2+b2+b1+d2+E1+f1+g2+e8 …………(8)
そこで因子Aの第一水準効果を求めるために1~4列のデータを合計すると
A1: x1+x2+x3+x4
=4μ+4a1+2b1+2b2+2c1+2c2+2d1+2d2+2E1+2E2+2f1+2f2+2g1+2g2+e1+e2+e3+e4 …………(9)
そして因子Aの第二水準効果を求めるために5~8列のデータを合計すると
A2:x5+x6+x7+x8
=4μ+4a2+2b1+2b2+2c1+2c2+2d1+2d2+2E1+2E2+2f1+2f2+2g1+2g2+e5+e6+e7+e8 …………(10)
よってA1データの合計ーA2データの合計は次の式となります。
= 4(a1 - a2 )+誤差 …………(11)
このように因子Aと誤差以外の要因がすべて消えてしまうために、因子Aの要因効果が抽出できるのです。因子BからGについても同様に、それぞれの水準一と水準二に対応する行を加算して差を求めるだけで、因子効果が求められます。
実際には(1)~(8)の誤差eには実験誤差、測定誤差の他に各因子間の交互作用効果も含まれているために、それが大きくなるほど(11)の誤差も大きくなり、そこで得られた推定効果が現実に合わなくなってしまいます。
だからといってこの極めて効率的な道具を放棄する理由とはならず、各種の工夫で対処することとなります。
...