♦ 数学の教科書に書いてある通りにプログラムしてもだめ!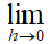 では計算できない!
では計算できない!
サイン・コサイン何になる…とか嘯(うそぶ)いていた学生時代。しかし「現場に出て数学の重要性をひしひしと感じているのに、確実な理解が出来ていない…」と不安を抱いている技術者の皆さん。そこで、今回から18回にわたり「本当に意味のある“現場数学”とは何か」について私ともう一度考えてみませんか?
1.“現場数学”では、hは有限でなければならない
高校で微分とか積分を習った時、先生が今まで見たことのない如何(いか)にも新しい式である![]() と黒板に書く様に感激した経験を思い出します。しかし、これでは本当は計算できないのです。「現場数学」では、hは有限でなければなりません。となると…小さい、と思われる数、例えば0.00001とかにすれば良いということでしょうか?いえいえ、全くそうではないのです。この辺りから疑問を感じていた人は多いのです。でも、高校の先生に聞くと、ムニャムニャとした返事。それで数学が嫌いになった人がいるほどです。どうなっているのでしょうか?
と黒板に書く様に感激した経験を思い出します。しかし、これでは本当は計算できないのです。「現場数学」では、hは有限でなければなりません。となると…小さい、と思われる数、例えば0.00001とかにすれば良いということでしょうか?いえいえ、全くそうではないのです。この辺りから疑問を感じていた人は多いのです。でも、高校の先生に聞くと、ムニャムニャとした返事。それで数学が嫌いになった人がいるほどです。どうなっているのでしょうか?
実はhは小さいどころか無限大でも良いのです!これは極端な話です。でも、高校数学で重要なことを教えていないことは確かなのです。また、大学に入ると微積分は途端にε-δの話になり、余計に誤魔化されてしまいます。実は、最初に考えなければならないのは対称性の問題なのです。通常の微分係数の記述は、
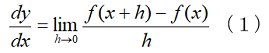
です。しかし、これでは、xの位置から正方向のみの変化を見ることになり、その位置で増加している関数なら当然、x点での値より大きくなります。それにも関らず なのだから、正しい値に近づくはずと習うのです。これは一種の詭弁(きべん)です。二次関数y=x2にこの微分係数の式を当てはめてみましょう。
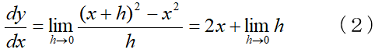
となります。hだけの誤差があり、 で正しい2xになるという論法です。実は、この公式は前進公式と呼ばれます。xから正方向だけをみているからです。x点での微分係数を求めたいのですから、-h方向もみないといけません。それは後退公式と呼ばれる次式です。
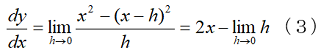
この式の誤差は-hです。ということは(2)式と(3)式の平均をとれば、hの大きさに依(よ)らず微分係数は2xと厳密に求まります。
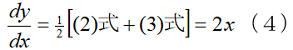
つまり微分係数はhに依らず、極端にいえばhは無限大でも良い式が作れたのです。この例では、2次関数の微分は一次関数ですから、hに依らず誤差が消えてしまいました。3次関数でも、何次関数でも同様に誤差を消してしまう公式が作れます。ぜひ、自分の手を動かして試して下さい。
2. より本質理解し、数式を上手に扱う
この例題は、教科書に書いてある通りの式をそのままプログラムして、数値計算してはいけないことを如実に示しています。「現場数学」では、数値をなるべく正確にしかも効率良く計算しなければなりません。それを身につけるためには、このような高校の教科書に載っていなかった方策を勉強する必要があります。これは、頭の良...