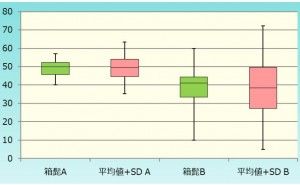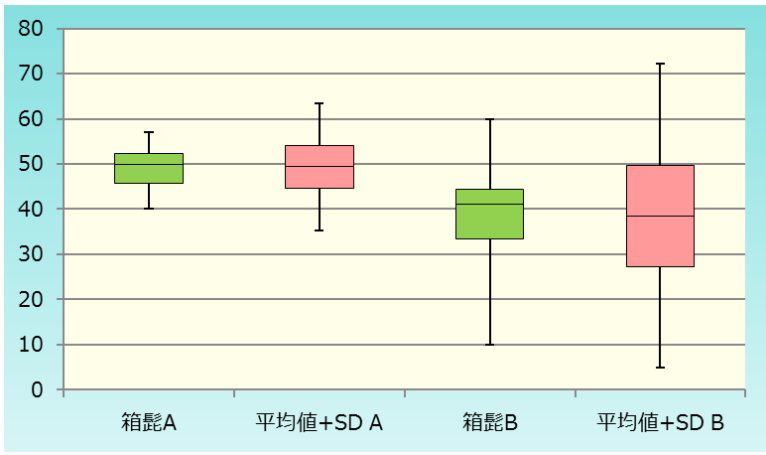
層別比較に便利なグラフ


続きを読むには・・・
この記事の著者

この記事の著者
眞名子 和義
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します
「SQC一般」の他のキーワード解説記事
もっと見る~速算:暗算計算と九去法 続・現場数学(その20)
♦ 計算を身近なケースから考える 1. 電卓よりはるかに速く~ 速算と暗算の活用 本シリーズのタイト...
♦ 計算を身近なケースから考える 1. 電卓よりはるかに速く~ 速算と暗算の活用 本シリーズのタイト...
~マルチスケール模型での計算 現場数学(その6)
1. 計算の限界 如何(いか)にスーパーコンピューターを活用しても、計算出来る範囲はやはり限られています。例えば、タン...
1. 計算の限界 如何(いか)にスーパーコンピューターを活用しても、計算出来る範囲はやはり限られています。例えば、タン...
基本統計量について(平均値・中央値・分散・標準偏差など)
数値データを分析するにあたり、情報の特徴を知るために基本的な統計量がありますので、今回はその中のいくつかについて説明します。 1.平均値(mean、a...
数値データを分析するにあたり、情報の特徴を知るために基本的な統計量がありますので、今回はその中のいくつかについて説明します。 1.平均値(mean、a...
「SQC一般」の活用事例
もっと見る飛行機事故とセンサー・フィードバックの分布
ボーイング 737 Max 8機が短い期間に2回の墜落死亡事故を起こし、多くの航空会社が同機種の運航を停止する事態となっています。多くの...
ボーイング 737 Max 8機が短い期間に2回の墜落死亡事故を起こし、多くの航空会社が同機種の運航を停止する事態となっています。多くの...
DPMOとは何か
DPMOとはDefects Per Million Opportunityのイニシャルを取ったものです。DPMOを百万個当りの欠陥数(製品百万個当りの不...
DPMOとはDefects Per Million Opportunityのイニシャルを取ったものです。DPMOを百万個当りの欠陥数(製品百万個当りの不...
統計教育が必須な検査担当者
測定や検査結果の値で合格判定を行い、製品性能の品質保証をする事は製造業に取っては当たり前と言える日常的作業です。一方で検査や測定の正確さや信頼性を担保す...
測定や検査結果の値で合格判定を行い、製品性能の品質保証をする事は製造業に取っては当たり前と言える日常的作業です。一方で検査や測定の正確さや信頼性を担保す...