調和平均と重みつき平均 平均のいろいろ（その2）

更新日 2022-08-10

投稿日 2019-02-05

SQC

SQC

SQC

SQC

  　続きを読むには・・・

新規会員登録

この記事の著者

村島 繁延

QCDはバランスさせるものではなく、全て両立させるものだという信念で向かいます。一石三鳥を狙った成果を目指します。

QCDはバランスさせるものではなく、全て両立させるものだという信念で向かいます。一石三鳥を狙った成果を目指します。

「SQC一般」の他のキーワード解説記事

もっと見る
転ばぬ先の杖～RFCの備え
転ばぬ先の杖～RFCの備え

　RFCとはResponse Flow Chart(若しくはchecksheet)の略語です。あまりポピュラーな用語ではありませんが、外資系の製造業では良...

　RFCとはResponse Flow Chart(若しくはchecksheet)の略語です。あまりポピュラーな用語ではありませんが、外資系の製造業では良...

～公式とは？ 現場数学（その4）
～公式とは？ 現場数学（その4）

  　力学、流体力学、電磁気学、光学、熱力学、統計力学、量子力学…、さらには遺伝子工学まで、多くの数学公式が現れ、その数値解...

  　力学、流体力学、電磁気学、光学、熱力学、統計力学、量子力学…、さらには遺伝子工学まで、多くの数学公式が現れ、その数値解...

層別比較に便利なグラフ
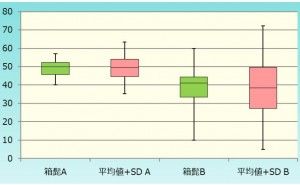
層別比較に便利なグラフ

　層別比較に便利なツールとしては、『箱ひげ図』があります。箱ひげ図は少数データの扱いも容易で作成も簡便なので便利ですが、分布の中心が中央値で、分布の幅がパ...

　層別比較に便利なツールとしては、『箱ひげ図』があります。箱ひげ図は少数データの扱いも容易で作成も簡便なので便利ですが、分布の中心が中央値で、分布の幅がパ...

「SQC一般」の活用事例

もっと見る
第1種の誤りと第2種の誤り
第1種の誤りと第2種の誤り

　｢あわて者の誤り｣と｢ぼんやり者の誤り｣をご存知ですか、あわて者の誤りは正式には『第一種の誤り』(Type Ⅰ error)と呼称し、ぼんやり者の誤りは...

　｢あわて者の誤り｣と｢ぼんやり者の誤り｣をご存知ですか、あわて者の誤りは正式には『第一種の誤り』(Type Ⅰ error)と呼称し、ぼんやり者の誤りは...

統計教育が必須な検査担当者
統計教育が必須な検査担当者

　測定や検査結果の値で合格判定を行い、製品性能の品質保証をする事は製造業に取っては当たり前と言える日常的作業です。一方で検査や測定の正確さや信頼性を担保す...

　測定や検査結果の値で合格判定を行い、製品性能の品質保証をする事は製造業に取っては当たり前と言える日常的作業です。一方で検査や測定の正確さや信頼性を担保す...

信頼できる結果を得るために統計的手法の活用を
信頼できる結果を得るために統計的手法の活用を

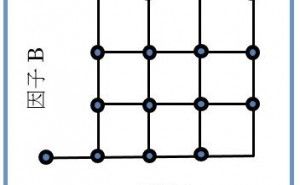
昔の事になりますが、配属された職場の先輩の下である実験を手伝いました。先輩は図1のような計画をたてました。2つの量的因子A、Bの効果を確認する実験でした。...

昔の事になりますが、配属された職場の先輩の下である実験を手伝いました。先輩は図1のような計画をたてました。2つの量的因子A、Bの効果を確認する実験でした。...