重回帰分析といえば説明変数が複数の回帰式をいいます。ものづくりの場面ではもちろん、マーケット調査や心理学など社会科学の分野でも活用されている一方で、単回帰分析ほどには多用されていません。ひとつには、難しいという先入観があります。それは、重回帰式のなかの係数を算出することが大変だという思いこみです。
しかし、実は、パソコンの普及した今日、大きな問題ではありません。むしろ、パソコンで出力された解析結果の無理解による「誤読」が問題です。この点は、今も昔もあまり変わりないかもしれません。むしろ、昔は、重回帰式の係数を算出できるようなレベルの人は、統計解析結果の読み方ぐらいはわかっているので、さほど大きな「誤読」（誤判断）はなかったのでしょうが、現在は、統計の基礎ができていない人でもパソコンで簡単に解析結果が出力される分、誤読は多くなるかもしれません。
以下では、二つのことを説明します。ひとつは重回帰分析の基本的なやりかたです。他は、主に「誤読」されやすい点への注意です。重回帰分析が役に立たないという人もいますが、大抵の場合は「やりかた」を間違っている場合が多いようです。又、やり方でなく「誤読」による勘違いで間違ったアクションをとったという場合もあります。
1．重回帰分析の簡単な方法
以下はエクセルによる解法です。
「データ」⇒「データ分析」⇒「回帰分析」OK としますと、下記画面が表示されますから入力範囲を入力します。Yは目的変数のことです。Xは説明変数ですが、複数個あるわけですから、全て選びます。（画面1.参照）
「データ」⇒「データ分析」⇒「回帰分析」OK としますと、下記画面が表示されますから入力範囲を入力します。Yは目的変数のことです。Xは説明変数ですが、複数個あるわけですから、全て選びます。（画面1.参照）
画面1「エクセルの回帰分析画面」
ラベルは変数名が1行目にきている場合にチェックを入れます。入れないと、何が何だかわからないので、普通はいれます。定数に0を使用は使ったり使わなかったりです。有意水準は、普通はこのままでおいておきます。有意水準ですから、95%というのはウソで、5%のことです。なぜか、こうなっています。昔から。よく、統計に詳しい人がわざわざ5%に変えたりすると、間違いのもとになります。
出力オプションを適当に選べば、その位置に結果がでてきます。これで終わりです。ただし、この重回帰分析を行う前には、事前に相関行列を確認し（これもエクセルでできます）、説明変数間の相関の高いものを外しておくことが大事です。多重共線性というものを防ぐためです。難しい言葉ですが、これがあると不安定な式だということです。信用できなくなります。さらに、説明変数間に相関が高いと、重回帰式の係数から目的変数との正負相関を見誤ります。これは非常に大きな誤用になります。この理由を2項にて説明します。又、経験的に目的変数との相関が0.2以下というのは重回帰分析をやっても意味のない場合が多いのでこれも外した方がいいです。
よくある質問に、必要なデータ数（連データ数：目的変数と説明変数の対応したセット数）の問題があります。数学的には「データ数－説明変数の数－1≧0」（式1）ですが、これは、あくまで数学上の方程式が解ける解けないことからきているので、不十分です。ばらつきまで考慮すれば、説明変数の10倍以上が必要です。たとえば、単回帰の場合、式1に従えば、データ数－1－1≧0 より、データ数≧2 となります。要はデータ数2個あれば、回帰式がきまるというものです。あたりまえですが、ばらつきがあれば使えません。単回帰の場合、30個程度が最低必要といわれています。
2．出力表の見方（誤読への注意事項：特に表3）
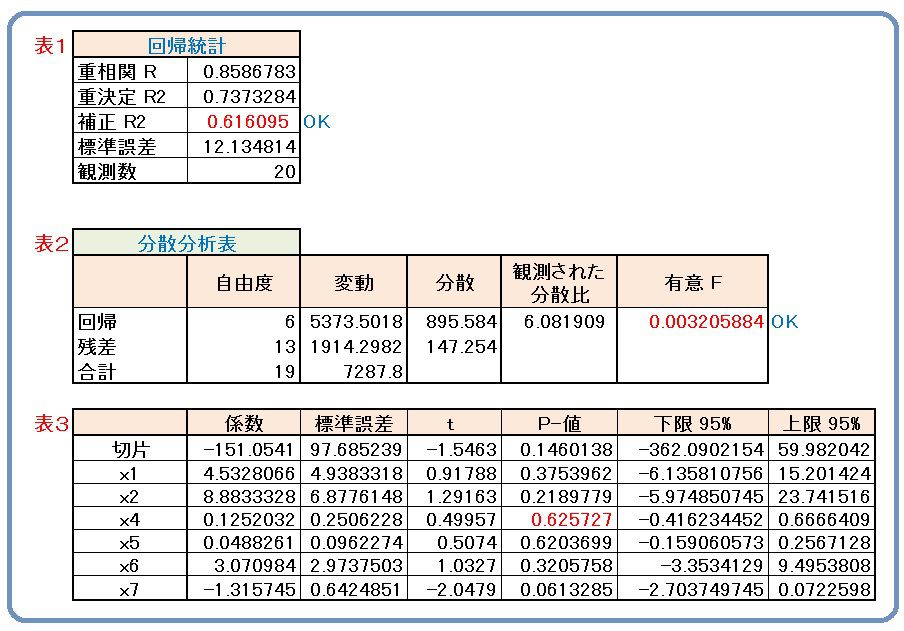
前項に従って、手順実行すれば図1のような出力表が出てきます。
図1.手順実行後の出力表
表1の重相関Rというのは、重相関係数のことです。通常、相関係数は－1から＋1ですが、このRは0から1です。x軸に観測値（実測値）をとり、y軸に予測値（回帰式から）をプロットした散布図を想定し、その相関係数をだせばRになります。その二乗を重相関決定係数（表では重決定）といい、R2で表しています。正確にはR2というものです。補正R2というのは、正式には「自由度調節済み決定係数」というものです。通常は、R*2と書きます。これは、データ数に比べて説明変数の数が多いときにみかけ上、決定係数Rが大きくなるので、こういう場合にこちらを使います。決定係数の計算に変動を使うか、分散を使うかの違いですが、変数選択をする際に、両にらみするのでともに有用です。
標準誤差は、実測値と予測値（回帰式から算定）の差をエラーと呼んだとき、エラーの平均的なばらつきの推定値です。標準偏差とは違います。
表2の分散分析表の見方で重要なものは有意Fのところでしょう。『切片以外の全ての説明変数の効果が0である』という帰無仮説のもとで、偶然によって標本が観測されてしまう確率の上限です。簡単に言えば、5%以下なら信用していいといえます。これが5%を超える結果というのは、よほど変な説明変数を取り上げたか、異常値を含んでいるか、線形でないもの（放物線とか）を選んでいるかです。一からやり直しです。通常は1%以下です。
表3の係数というのは、偏回帰係数のことです。これが重回帰式の係数です。よくある誤読に、この係数の見方が挙げられます。以下はその典型です。
ⅰ. この係数が大きければ効果が大きい。
ⅱ. この係数がプラス（マイナス）ならば目的変数と説明変数は正相関（負相関）である。
ⅱ. この係数がプラス（マイナス）ならば目的変数と説明変数は正相関（負相関）である。
⇒ⅰは、変数1と変数2で単位が違う場合を考えれば、明白です。grとcmでは比較のしようがありません。この場合、データを標準化して、同様の解析を行い標準偏回帰係数を算出すれば、単位は消えて、係数の大小で効果の大きさが推定できます。（有意性はとなりのt値やp値を見ます。t値が大きく、p値が小さく、標準偏回帰係数が大きいほど、効果が大きく、有意性が高いといえます。）
⇒ⅱは多重共線性に関連していますが、簡単な説明でよければ、次のように考えます。
重回帰式で、説明変数x1、x2 とし、目的変数yとしたとき、y=x1－x2 （式2）となったとき、yはx1と正相関、x2と負相関といえるかどうかです。単回帰なら、そうも言えますが、重回帰ではそうとも限りません。x1とx2に相関が強ければ、x1＝2・x2 （式3）これを式2へ代入すれば、
y=2x2－x2=x2 （式4）
yはx2と正相関になります。こういった煩雑な判断が誤判断のもとになります。これを防ぐには、相関係数の高い説明変数のうち、どちらかを外すことです。外し方について...
ZoomやSkypeなどのネット配信ツール
