「主成分分析」とは、キーワードからわかりやすく解説

1. 「主成分分析」とは

主成分分析とは、多変量からなるデータのいくつかの変量に共通して含まれる要素を抽出するための統計的分析法です。 これによって抽出された要素を主成分と呼び、主成分どおしは互いに無相関です。 この分析によって、元々多数の変量で表されていたデータを、少数の主成分軸に投影した主成分スコアで表現する事が可能となり、特徴を理解しやすくなります。

2.  「主成分分析」の基本原理

 「主成分分析」は、多変量データの主要なパターンを把握するための技術であり、特に次元削減に用いられます。次元削減であって、特徴量選択ではありません。主成分分析では、元の特徴量から新しい特徴量セット（主成分）を作成します。これらの主成分は、データの最大の分散を捉えるように設計されており、互いに直交（独立）しています。新しい特徴量セット（主成分）が、元の特徴量よりも、その変数の数が少ないというものです。

3. 「主成分分析」とクラスタ分析

「主成分分析」とクラスタ分析は、データを集約（もしくは、グルーピング）する分析技術の1つです。主成分分析は変数（データセットの列）を集約（もしくは、グルーピング）することで次元縮約（例：1,000変数を10変数にまとめる）するのに対し、クラスタ分析はケース（データセットの行）を集約（もしくは、グルーピング）することで似たようなケースをクラスタ化（同じようなのが集まっている状態）します。この場合のケースとは、個体（例：個人や店舗、企業など）です。ちなみに、主成分分析で作られた新たな変数を「主成分」と呼びます。

4. 主成分の具体的な抽出方法：分散の最大化と直交性

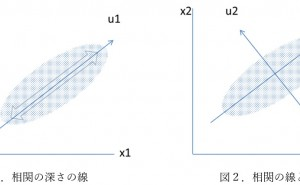
主成分分析（PCA）の核心は、データの分散を最大化する方向を見つけ出すことにあります。最初の主成分（第1主成分）は、元のデータセットの変動を最もよく説明できる、つまり最も分散が大きい方向（軸）として定義されます。

具体的には、元のデータセットの共分散行列を計算し、その固有値と固有ベクトルを求めることで主成分を抽出します。固有値は、その対応する固有ベクトル（主成分軸）が捉える分散の大きさを示します。固有値が大きいほど、その主成分はデータの多くの情報を保持している、と解釈できます。

第1主成分が決定された後、第2主成分は、第1主成分と直交し（無相関）、かつ、残りの分散を最もよく説明できる方向として計算されます。この「直交する」という制約が、主成分同士が互いに独立であること（無相関）を保証します。以下、第3、第4と、元の変数の数だけ主成分を計算することが原理的には可能ですが、実用上は、累積寄与率が一定の値（例えば80%や90%）を超えるまでの少数の主成分を採用することが一般的です。この作業こそが、PCAが強力な次元削減手法である所以です。

5. 主成分分析の適用例と解釈の重要性

主成分分析は、データに含まれる潜在的な構造を明らかにするために、多岐にわたる分野で活用されています。

マーケティング・顧客分析: 顧客の購買データやアンケートの回答項目といった多数の変数から、「価格重視」「品質志向」「トレンド追従」といった、より抽象的な**潜在的な顧客特性（主成分）**を抽出します。これにより、複雑な顧客データを少数の指標で要約し、ターゲット戦略の立案を容易にします。
画像処理: 画像はピクセルごとの色の値という高次元のデータとして扱われますが、PCAを用いてノイズ除去やデータ圧縮を行うことができます。
金融: 多数の株式の騰落率データから、市場全体の動きや特定のセクターの共通した変動パターンといった、隠れたリスク要因を抽出・分析します。
PCAで重要なのは、単に次元を削減することだけでなく、抽出された主成分が何を意味しているのかを解釈することです。主成分スコアだけでなく、元のどの変数がその主成分の形成に強く影響しているかを示す因子負荷量（ローディング）を確認する必要があります。例えば、「価格重視」という主成分に対して、「割引商品の購入頻度」という変数の因子負荷量が大きければ、その解釈の正当性が裏付けられます。この解釈作業は、統計的な計算能力だけでなく、分析対象分野の専門的な知識が求められる部分であり、PCAを実務で活用する上での肝となります。

6. 主成分分析の限界と注意点

主成分分析は非常に有用ですが、万能ではありません。適用する上で、いくつかの限界と注意点があります。

第一に、PCAは線形な関係しか捉えられません。データに非線形な構造や複雑なカーブ状のパターンが含まれている場合、PCAではその構造を効率的に圧縮・抽出することが難しい場合があります。その際は、カーネルPCAなどの非線形次元削減手法が検討されます。

第二に、PCAは元の変数が同じ単位やスケールを持っていることを前提としていません。例えば、一つの変数が「身長（cm）」で、別の変数が「年収（円）」のようにスケールが大きく異なる場合、分散が大きい変数（この例では年収）が主成分の抽出に過度に影響を与えてしまうことになります。そのため、PCAを適用する前には、通常、全変数を平均0、分散1に変換する標準化（Z-score化）などの前処理が必須です。

最後に、PCAは分散を最大化する軸を探すため、その軸が必ずしも「最も分類に役立つ」軸であるとは限りません。特に、教師あり学習の文脈で「分類」や「予測」を目的とする場合、PCAは必ずしも最適な前処理ではない可能性があります。分類性能の向上を目的とする場合は、線形判別分析（LDA）など、クラス間の分離を最大化する手法の方がより適切である場合もあります。PCAはあくまで、データの構造を要約・可視化するための強力な探索的データ分析ツールとして位置づけられます。