
【この連載の前回:レオロジーを深く知る(その3)レオロジーという「考え方」へのリンク】
◆連載記事紹介:ものづくりドットコムの人気連載記事をまとめたページはこちら!
第2章 簡単な数学と物理的事項
第2章では「レオロジーをはじめる前に」として、レオロジーの理解に向けて必要な下準備を進めていきます。数学および物理の基本的な考え方に焦点を当て、読者がついていけるように心がけます。以下に、この章で取り扱う要点を簡潔にまとめてみました。
【この章で取り上げる内容】
• 数学的な事項の確認
– 「関数」の基本的な理解
– 事象をシンプルに考えるときに欠かせない「線型性」
• 物理的な視点に必要になること
– 物理モデルと線型性
– 物理モデルを理解するための「量」「次元」「単位」
1. 数学的な事項の確認から
具体的なレオロジーの議論に入る前に、今後の話に不可欠な数学の基本を振り返っていきましょう。それほど難しい内容ではありません。中学から高校の基礎的な事柄に戻り、レオロジー理解に欠かせない基本を再確認していただくことが目的です。具体的には、「関数と線型性」に焦点を当て、分かりやすく説明しますので、少しずつイメージを明確にしていくようにしましょう。
1.1 関数について
1.1.1 直感的理解
関数の概念を直感的に把握しましょう。関数は、変数xとyがあり、入力xを与えるとそれに基づいて出力yが得られるというルールです。関数は入力を変換する装置であり、入力と出力の関係性を示しています。
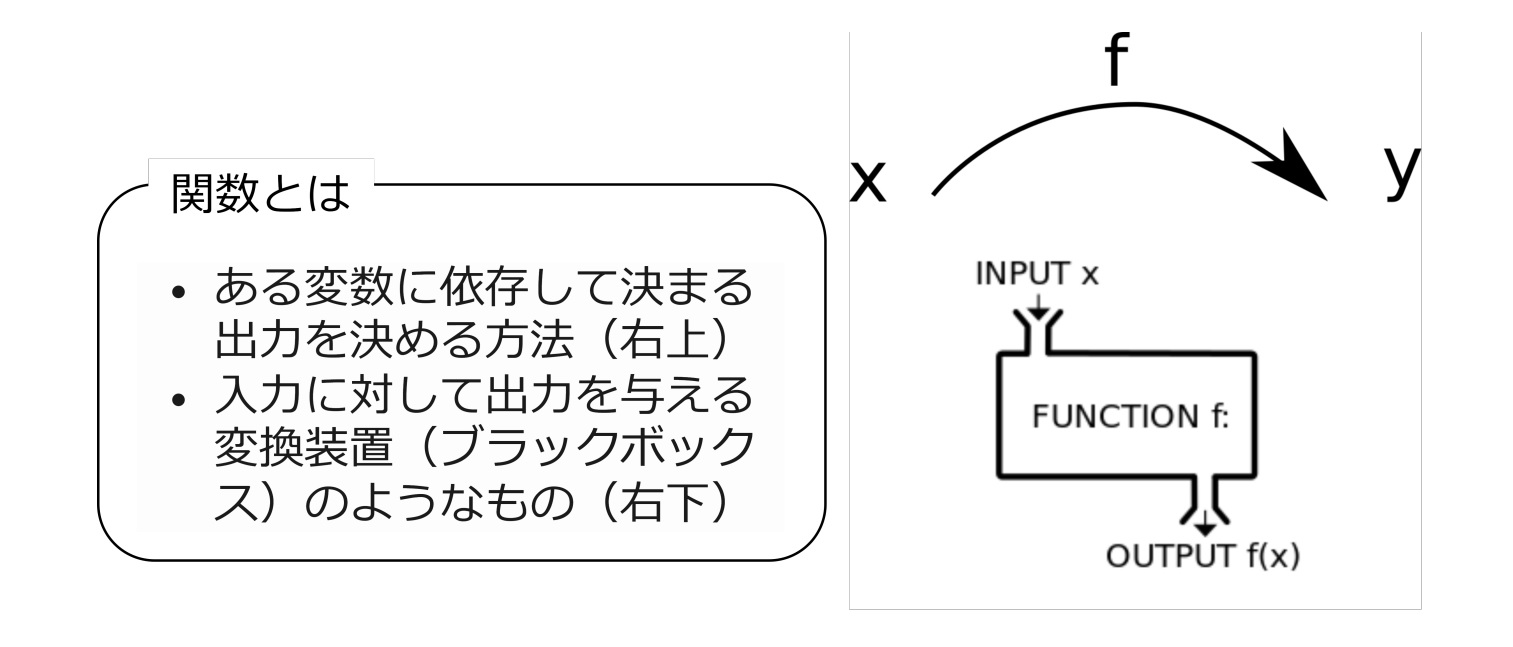
図1. 関数のイメージ
一般に、関数は英語の function の頭文字を使って fで表され、使用する変数がカッコの中に示されます。
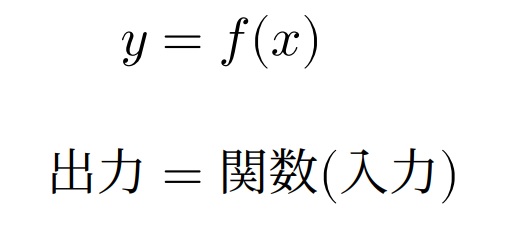
1.1.2 関数と写像
関数は、数の集合に値を対応させる一種の写像と見なすこともできます。定義域と呼ばれる左の集合から値域となる右の集合への射影が、関数の本質です。
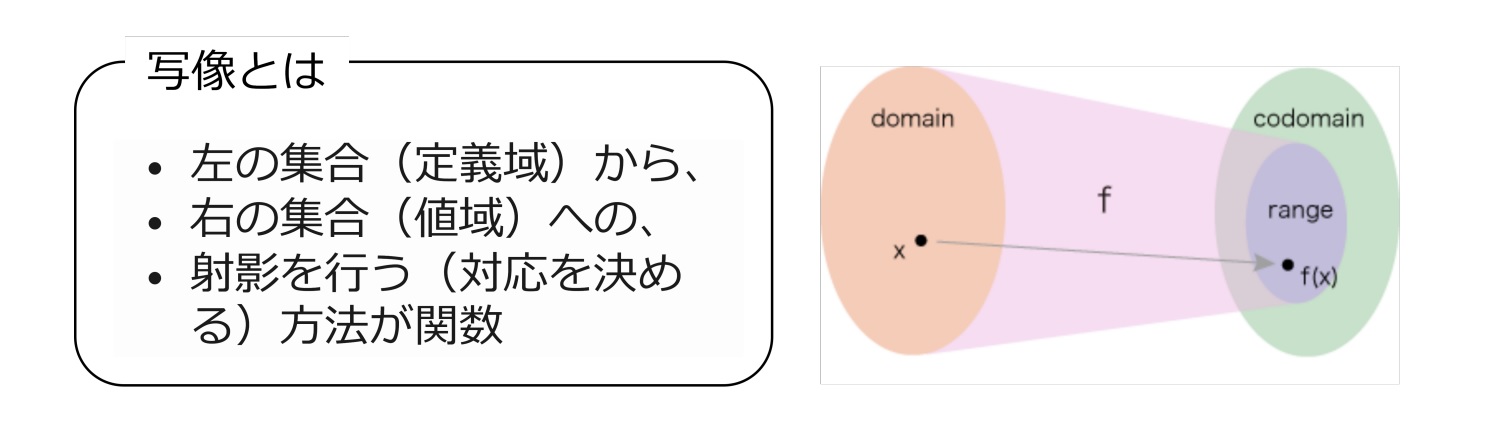
図2. 関数と写像
1.1.3 グラフとは
グラフは、入力と出力の関係を平面図に示したもので、その関係を視覚的に理解しやすくしたものです。具体的には、入力xに対応して決まる出力の点を平面上にプロットし、それを連続的に線で結んだものがグラフです。
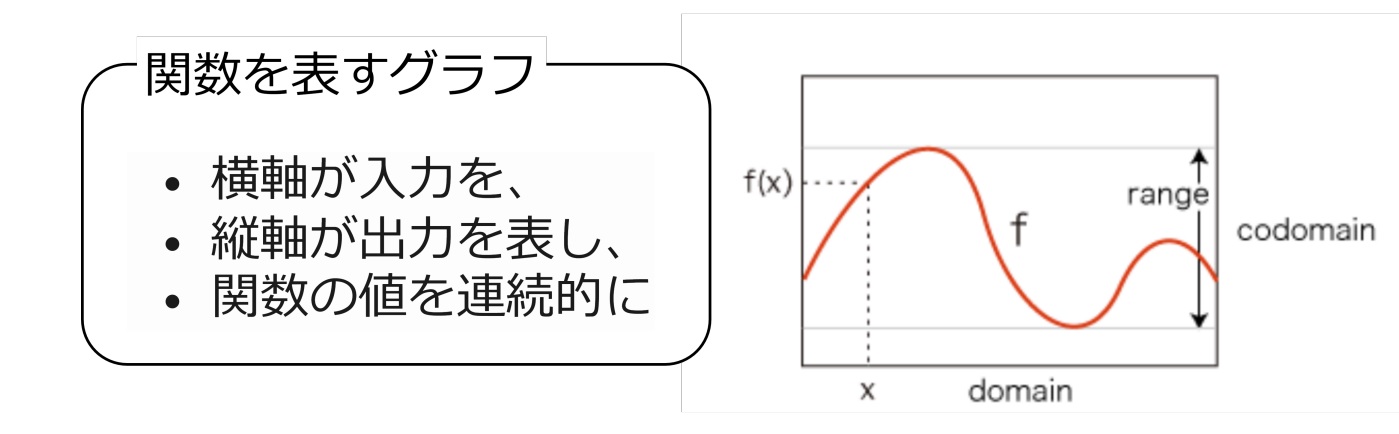
図3. 関数とグラフ
図2 に示した集合間の写像を 2 次元のグラフに表すと、図 3 のようになります。グラフに表した関数の形を見ることで、入力と出力との関係を直感的に理解できます。
1.2 線型という意味を理解しよう
1.2.1 線型とは?
線型性を直感的にイメージすると、グラフに表した時に原点を通る直線として現れる性質です。数学的に正確に説明すると、関数などの演算 fが以下の 2 つの性質を満たす場合、 fは線型性を持つと言います。線型性を表す性質は以下の通りです。
• 加法性:任意の x, y に対して
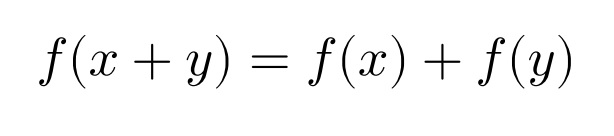
• 斉次性:任意の x, a に対して
![]()
線型性を示す関数は多く存在し、代表的なものは以下のような一次方程式です。
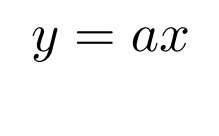
これは、入力が倍になると出力も倍になる比例の関係を表しています。また、加法性は小学校の応用問題である旅人算にも応用されます。
1.2.2 線型性の意味
線型性が成立することで何が嬉しいのでしょうか。小学校レベルの簡単な問題を考えてみましょう。「水道の栓を開けて、浴槽に水を溜めています。5 分間流して 100L の水が溜まりました。
このとき、1 分間流したときには何 L 溜まっていたでしょう?」と聞かれたとすると、比例の関係から 1 分 ×100L/5 分=20L と答えることができ、これは、過去を推定していることになります。同様に、「10 分では、何 L 溜まるでしょう?」では、未来のことを予測できます。
また、「浴槽に 2 つの蛇口から水を溜めていきます。A という蛇口からは 1 分間で 20 L、B という蛇口からは 5 分間で 150 L の水を貯めることができます。両方の蛇口から同時に水を溜めたとき、10 ...





































