相関行列という言葉は、QC7つ道具ではでてきませんが、散布図の説明に相関係数という単語が使われます。散布図は一つの目的変数(y)と一つの説明変数(x)を縦軸、横軸で二次元表現したものです。相関図という単語はないと思っていましたが、信頼性用語では使われているようです。このことばのほうがぴんときます。相関を調べたいときにプロットすることが多く、散らばらすという意味での散布図という言葉は、目的からはそぐわないと感じています。その散布図を多変量にした場合、説明変数と目的変数、目的変数同士の相関係数が計算されます。この計算方法は単相関の場合と同じです。同じ変数同士なら相関係数は1となります。別の変数との相関係数はそれぞれ計算されます。
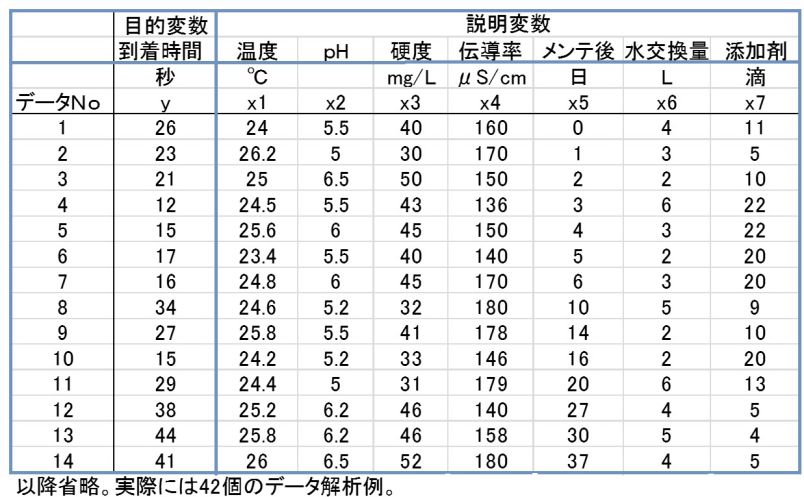
たとえば、下表1はある特性値(私の趣味の例で、エビが餌に集まってくる時間を目的特性yとし、その時の飼育環境や条件をx1・・・・x7 としています)の連データ(1対1対応)を示しています。
表1 エビが餌に集まる時間と飼育環境条件のデータ
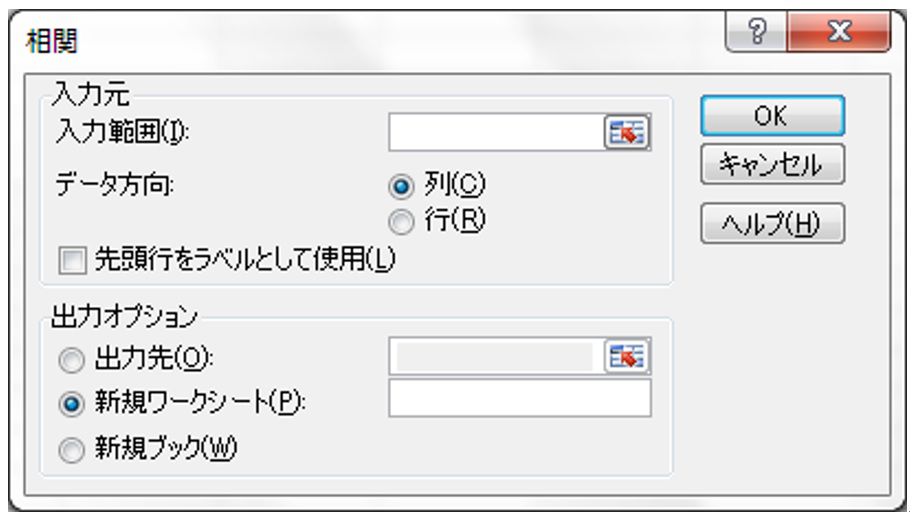
ここから、エビが一番早く餌に到着する条件を見いだそうというものです。実際にはT法や重回帰分析を使いますが、ここでは相関行列の説明のみに絞ります。相関行列は2対の変数で実施すればいいだけですから難しくありませんが、単相関を順番に計算していくと、8個から2個の組合せとして、28通りになります。これはエクセルでも簡単にできます。Excel→データ→データ分析→相関、OKでいけます。相関とあるのは相関行列のことです。下図1を参照してください。
図1 相関行列のためのExcel画面
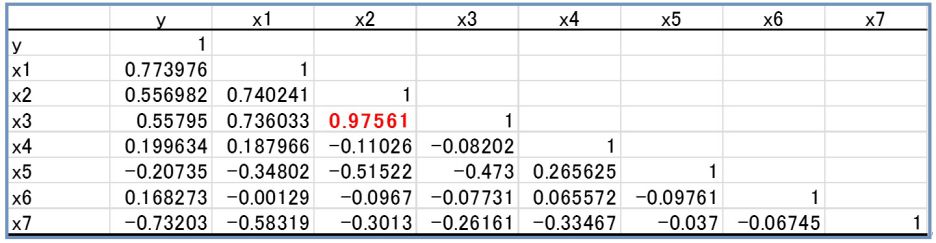
入力範囲をクリックし、実際の連データを選んでOKクリックすれば、表2のような相関行列が表示されます。
表2 相関行列の例
この表2において右上三角形部分は左下三角形部分と一致しますから、空白となっています。相関行列の作成方法は以上です。この相関行列は数値のみですが、異常値などが入っていると相関が高くなったり、逆に低くなったりしますので注意しましょう。ここではそのチェックは終わったとします。
次に使い道ですが、まず、目的変数と関係の深そうな説明変数がわかります。このことにより、単相関の情報よりも多くの情報を得ることができます。又、説明変数間で相関係数が高いもの、低いものも一目でわかります。重回帰分析やMT法等を使う場合には、多重共線性というくせものに注意しないと、結果が不安定になります。多重共線性は、説明変数間の相関係数が高いときに発生します。とくに相関係数が0.85以上あると要注意です。表2ではx2とx3に出ています。こういうことが起きると、例えば重回帰分析などでは、式の不安定さに加え解釈が煩雑で誤解釈しやすいものです。
たとえば、y=x1ーx2(式1)であれば、yはx1 と正相関、x2 と負相関と判断しがちですが、x1 とx2 に高い相関があって、x1=2x2 が成立しているとすれば、y= x2(式2)となりますから、yはx2 と正相関です。重回帰分析といっても、係数の誤差が大きい場合が多く、あまり信用していない人もいると思いますが、正相関か負相関かぐらいは当てにしてフィードバックすると思います。しかし説明変数間に高い相関がある場合には、当てにならないということになります。対策は簡単です。どちらかを外せば済みます。制御しやすい、コストのかからない、管理のしやすい変数を残すわけです。どっこい、どっこいなら目的変数との相関が高い方を残します。
この「相関係数の高いものチェック」は、MT法でも判別分析でも...