♦ 発想の転換で“桁落ち”回避
有限桁数の計算機を使って計算することによって起こる深刻な問題の例を挙げましょう。まずは、簡単そうに見える級数展開の問題を考えます。例えば、e-10を求めたいとします。それには、指数関数の級数展開
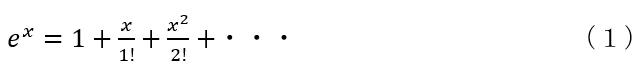
を用いて、C、BASIC、Fortranとか何らかの言語でプログラムを作成し、xに-10を代入して計算を実行すれば良いだけのはずです。パソコンでも、あっという間に収束し、
e-10=0.00055095・・・ (2)
という値が得られます。簡単ですよね?しかし、e-10の本当の値は、何と一桁も違って、
e-10=0.0000454・・・ (3)
なのです。プログラムを何度見直しても間違ってはいません。では、何故、どこも間違っていないのに全く異なる答えが出るのでしょうか?その原因は「桁落ち」です。実は(1)の公式で、xに負の大きな値を指定すると、展開の最初の数項にわたって正と負の大きい値が交互に現れ、それらの差し引き合計として、極めて小さい値が得られるのです。32ビットの精度で計算した途中結果は以下のようになります。
-9.00000000
41.00000000
-125.6666560
290.99975600
-542.33349600
846.55517600
-1137.57178000
1342.58691000
-1413.14478000
1342.58667000
-1162.62256000
925.05297900
-680.85205100
466.22338900
-298.49365200
179.45434600
-101.69165000
54.50067140
・
・
・
0.00055852
0.00054884
0.00055153
0.00055080
0.00055099
0.00055094
0.00055096
0.00055095
0.00055095
0.00055095
と約40項目で収束します。ところが、32ビットの数値を10進数で記述すると、実は6桁程度しか精度がないのです。そのため、途中の13桁ほど書いている部分の小数点以下には意味がないことが分かります。すなわち、収束して得られた値である0.00055095・・・という数値には何の意味もないのです。
では、どうやって、 e-10の値を正しく求めるのでしょうか?倍精度で解決。これも一つの手です。しかし、そういう力ずくではなく、実に発想の転換によって可能となるのです。つまり

を使うのです。正の値の指数関数の級数展開は問題なく収束します。その逆数を求めることによって、正しい値が得られるのです。
似ている他の問題として、正負が交互に現れる交代級数の和の値の求め方として、正の値と負の値を別々に集めて計算し、その結果得られた2つの値の差によって桁落ちを免れた正しい値を得るという方法も良く使われます。

も有名な例題です。この問題には、倍精度も何も効きません。何倍精度であろうと収束した結果は全て間違いなのです!ご存知のように、(5)の結果は無限大で、数値計算で求めることは出来ません。
...